math – Super Facts

Super fact 53 : The Euler number denoted e, is an irrational number, which like the number pi is extremely important in mathematics. In addition, the relationship between the Euler number and pi; seemingly unrelated numbers, is quite amazing, especially if you throw the imaginary number: i = square root of -1 into the mix. Euler’s formula e^ix = cos(x) + isin(x), where x is degrees expressed in radians, is mind blowing to say the least. Radians means that 180 degrees is replaced by pi, and 90 degrees is replaced by pi/2, etc. A simpler special case, but equally amazing is Euler’s identity e^ix = -1, or e^ix + 1 =0. This is amazing math assuming you understand it.

As I said all this is amazing, mind blowing if you will, if you understand it, which is why I will try to explain it. Why I consider this a super fact is because when you first encounter the Euler number and the Euler formula, and you somewhat understand what it means, it is likely to be a mind-blowing experience. Those among you who have studied higher math, AP math classes in high school, or college level math are probably familiar with what I am about to describe, so your mind may not be blown. By the way you pronounce Euler like “Oiler”.

The formula e^ix + 1 =0 shown on a blue and black background | The Euler Number Math Magic — Euler’s formula in cyber space with grid 3d illustration, Asset id: 1636161301 by Giggle2000

Euler’s Number and Pi Two Irrational Numbers

Pi is the number you get when you divide the distance around a circle (the circumference) by the distance across the middle (the diameter). The Euler number is a bit more complicated to explain. I will do that next. Both pi and the Euler number are irrational numbers, which means that when written as a decimal, the number neither terminates nor repeats. As I mentioned, both pi and the Euler number are extremely important numbers in math. Perhaps the Euler should have its own day, just like pi has its own day (March 14). Maybe we should start celebrating Euler number day on February 7.

The picture shows a circle and a brief explanation of what pi is. The 20 first decimals of pi as well as the 20 first decimals of the Euler number are shown. — The first 20 decimals of pi and of the Euler number.

Exponents

Before I explain what, the Euler number is, I need to explain what an exponent is. If you multiply a number by itself x number of times, then x is the exponent. If you multiply two by itself four times 2*2*2*2, called 2 raised to 4, then 4 is the exponent. By the way the answer is 2^4 = 16 (called 2 raised to 4 is 16). I hope the illustration below will explain it.

This picture explains what an exponent is. — Overview of exponents.

And finally, before explaining what the Euler number is I should also mention what a factorial is. The factorial of a number is the product of all positive integers less than or equal to that number. The factorial of 5 is denoted 5! and is 1*2*3*4*5 = 120. Also, the factorial of 0 or 0! = 1 (per definition).

Definition of the Euler Number

One more thing I need to explain before I go ahead with the definition for the Euler number is what is meant by allowing a number n in a formula to go towards infinity (limit –> infinity). Let’s say you have a formula that contains the number n. If the value of the formula does not change much as n becomes very large than it might be approaching a specific number as n approaches infinity. You say that it approaches a limit. I am trying to illustrate this in the picture below.

The formula (1 + 1/n)^n is given for a lot of different numbers n. You can see that a number, a limit, is reached as n approaches infinity | The Euler Number Math Magic — As the number n gets bigger the formula stops getting bigger and instead approaches a limit. When n approaches infinity that will be a very specific number. Which number do you think it is?

The picture features the definition of Euler’s Number as well as another formula consisting of an infinite sum that is also Euler’s number. — The definition of Euler’s number plus an infinite series sum that is also the same as Euler’s number.

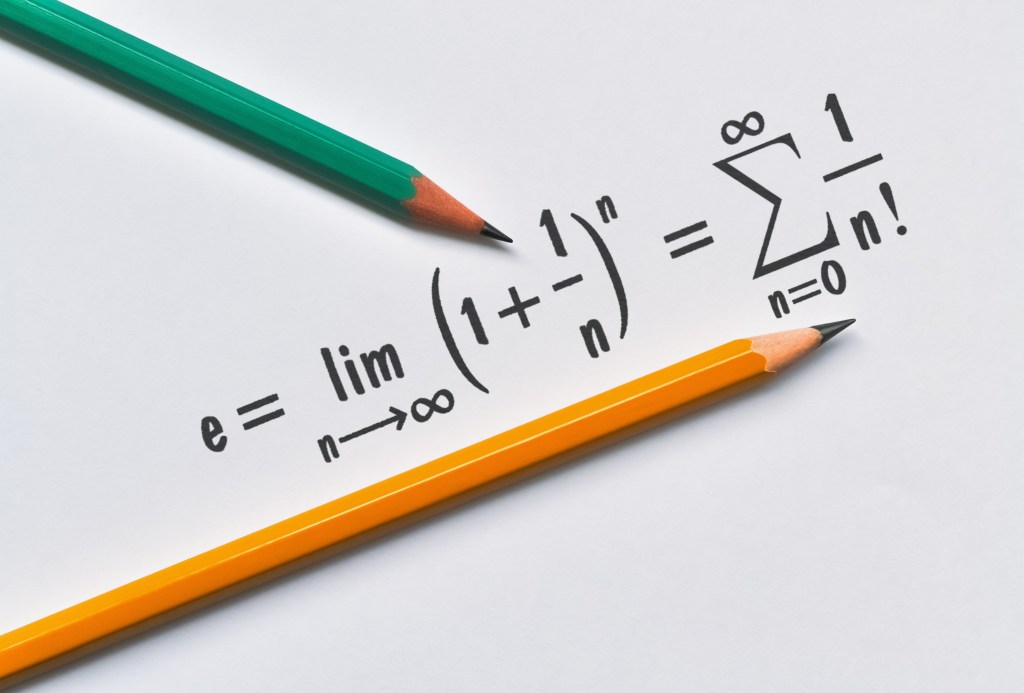
Two formulas equal to Euler’s Number. One is an exponent approaching infinity and the other is a sum from 0 to infinity | The Euler Number Math Magic — Definition of the Euler’s constant in two different ways, Asset id: 1227561829, by benjaminec.

Euler’s Number in Calculus

As I mentioned, Euler’s number shows up in mathematics in a lot of places. It is an extremely useful number with some amazing properties and that includes calculus. However, explaining functions and calculus may be going a bit too far, so I am just going to simply state that the derivate of e^x is just e^x and the indefinite integral, or the anti-derivative of e^x is e^x. In other words, differentiation / integration does not change this function. It also means that the slope of the curve is the same as the curve itself. Among all the infinite number of functions this is only true for e^x.

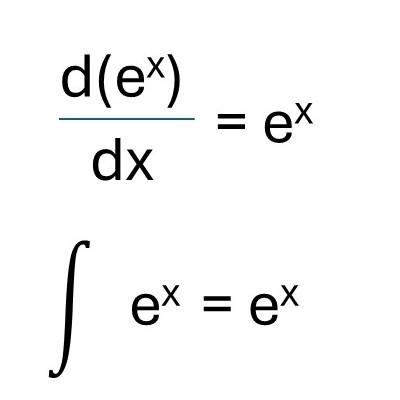
Differentiation and integration formulas for the exponential function. — Differentiation and integration does not change the function e^x.

Trigonometric Functions

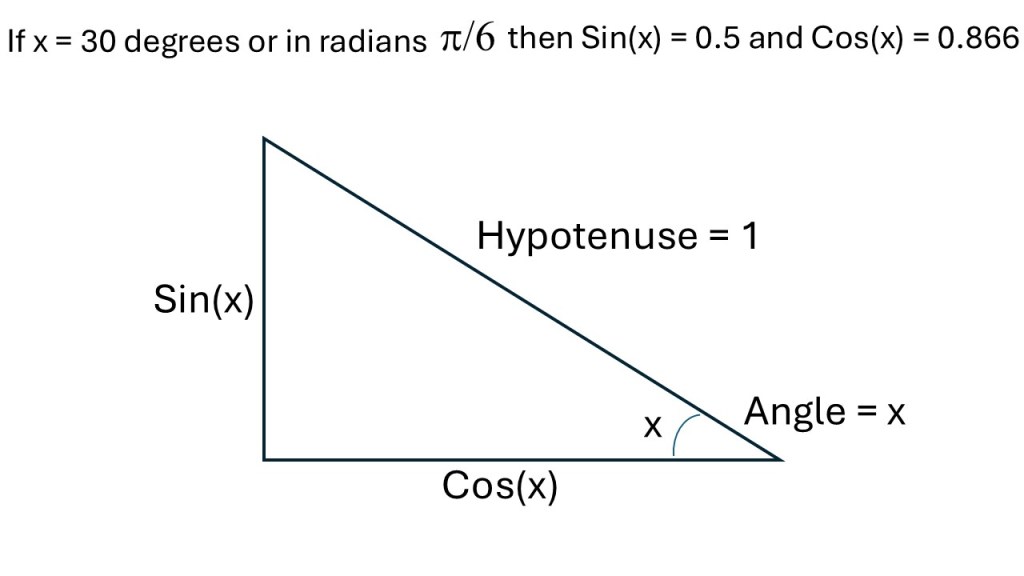
Next, I would like to launch into Euler’s formula. However, before I do that, I need to explain what trigonometric functions and imaginary numbers are. The trigonometric function sin(x) is the ratio of the length of the side opposite to a given angle to the length of the hypotenuse. In other words, if the hypotenuse is equal to 1, then sin(x) is the length of the opposite side to the given angle. The trigonometric function cos(x) is the ratio of the side of the triangle adjacent to the angle divided by the hypotenuse. In other words, if the hypotenuse is equal to 1, then cos(x) is the length of the adjacent side to the given angle.

Sin and cos are always between 1 and -1. ‘x’ is often expressed in degrees going from 0 to 360 (or 0 to 90 in a right-angled triangle). However, there is another way to express angles in triangles and that is radians. In this case the number pi corresponds to 180 degrees, pi/2 corresponds to 90 degrees, pi/4 corresponds to 45 degrees, etc. Euler’s formula uses trigonometric functions, but it only works if you use pi instead of degrees. Pi and Euler’s number have a special relationship. Sin and cos are illustrated in the picture below.

The picture shows a right-angled triangle with the sides being the hypotenuse set to 1 and the two other sides sin(x) and cos(x) respectively | The Euler Number Math Magic — Illustration of the trigonometric functions sin(x) and cos(x).

Imaginary Numbers

The last thing I need to explain before demonstrating Euler’s formula is imaginary numbers. The square root of a number is another number that, when multiplied by itself, equals the original number. For example, the square root of 4 is 2, because 2 * 2 = 4. The square root of 9 is 3, because 3 * 3 = 9. As long as you deal with real numbers, square roots must be positive numbers because you cannot multiply two numbers and get a negative number. -2 * -2 is 4, not -4.

However, that did not stop some mathematicians from making up a square root that was negative. This imaginary number is the square root of -1 and is referred to as i, yes just i, for imaginary. So, what’s the point of making up numbers that can’t exist? Well, it turned out to be quite useful and you can manipulate imaginary numbers to result in real numbers. For example, if you multiply the imaginary number i by itself i*i you get -1. If you multiply i by itself four times, in other words i^4, or i raised to 4, you get 1. Even more impressively, i raised to i, or i^i, is a real number. i^i = 0.207879… This is illustrated in the picture below.

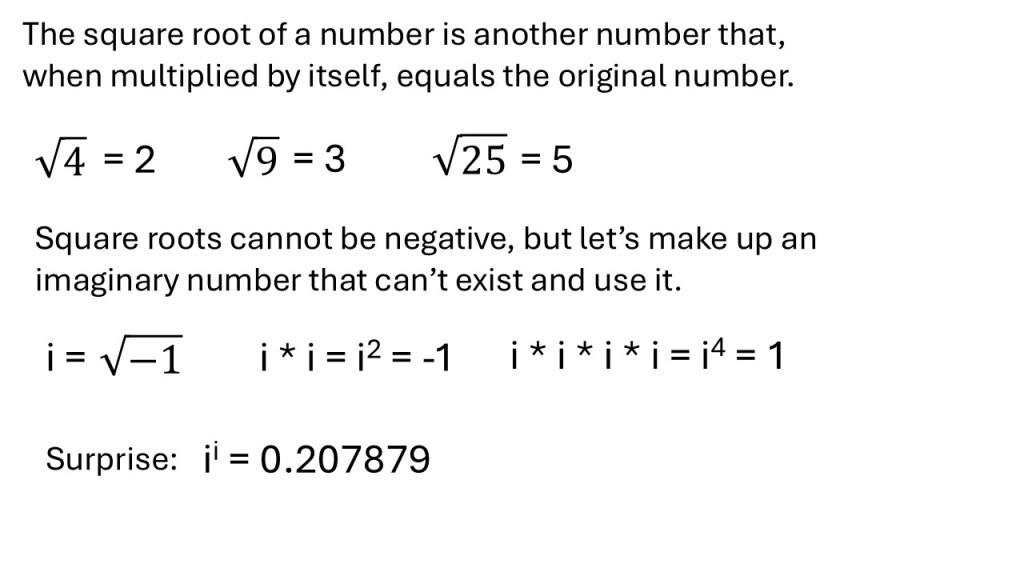
The picture features the definition of the imaginary number and an explanation for what imaginary numbers are, as well as examples. — Imaginary numbers illustrated

Eulers Formula

Without giving the proof, or any detailed explanations, below is Euler’s identity and Euler’s Formula (e^ix = cos(x) + isin(x)). Notice the mix of Euler’s number, pi, the trigonometric functions using radians (based on pi), and the imaginary number. Well, likely mind-blown, if you have not seen it already and you understood this post up to here.

The picture shows Euler’s formula illustrated in the complex plane. — Euler’s formula illustrated in the complex plane. Asset id: 2345669209 by Sasha701

If you want to see how you prove Euler’s Formula check out this youTube video.

If you want to learn more about the importance of Euler’s number in sommon and useful mathematics, check out this youTube video.

To see the other Super Facts click here

Super fact 36: Every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This revolutionary insight was mathematically proven in 1915 by a relatively unknown woman, Emily Noether.

It is not easy to understand what this super fact means, and therefore it is easy to miss the fact it says something fundamental about the nature of reality. It says something profound about our Universe and all possible Universes. It is arguably one of the most profound discoveries in science. Since the discovery of Noeth e r theorem, we do physics differently and we view our physical reality differently.

In the book “The Theory of Almost Everything” the author, theoretical physicist Robert Oerter states that the standard model of elementary particles, or most of modern physics, rests on three pillars, special relativity, quantum physics, and Noether’s theorem. Which one of those three have you not heard of? I guess Noether’s theorem.

That question brings me to the second part of the super fact. Emily Noether did a lot for mathematics and physics in addition to her first theorem (stated above), and yet she is not well known. Albert Einstein said of Emily Noether : “Fräulein Noether was the most significant creative mathematical genius thus far produced since the higher education of women began”. Notice he didn’t say “woman genius”.

Why I consider Noether’s (first) theorem a super fact is because it tells us something fundamental about reality that is highly surprising and yet undisputable (mathematically proven) and not many of us know about it. The second part of the super fact, that despite being one of the greatest geniuses of the 20th century she is so unknown, is also surprising.

A young woman in Victorian clothing sitting at a small table. — This picture reminded me of Emily Noether a genius and one of the greatest mathematicians in human history. This is a submission for Kevin’s No Theme Thursday.

Noether’s Theorem What Does It Mean

Noether’s theorem, says that symmetries in the universe give rise to mathematical conservation laws. One way to understand this is by using an example. That the physical laws remain the same as you translate a system in time is an example of a continuous symmetry.

If you do an experiment twice at two different times, let’s say at 8:00AM and at 9:00AM, and everything is set perfectly identical both times you are likely to get the same result. Well barring statistical/quantum uncertainty. The point is that the physical laws did not change. If the physical laws do not change between 8:00AM and 9:00AM, then you have a continuous symmetry.

Noether’s theorem says that if you have a continuous symmetry, you also have a conservation law, and the conservation law in this case is the conservation of energy/mass. If the physical laws do not change between 8:00AM and 9:00AM then mathematically the total energy / mass of the closed system must remain constant.

It follows that energy is not destroyed or increased. At first it seems like the time symmetry and energy/mass conservation have nothing to do with each other, but the symmetry gives rise to the conservation law. So, if you ask the question, why is energy / mass conserved, the answer is because physical laws don’t change with time.

There are many symmetry-conservation law pairs in nature. Translational symmetry, the fact that the laws of physics stay the same if you move to the side or forward, results in the conservation of momentum. The symmetry of laws that does not change if moving around in a circle amount to the law of conservation of angular momentum. Other symmetries result in the conservation of charge.

The converse is also true. If you find that a quantity is conserved you can find a symmetry, and if you find a symmetry that is broken you can find a quantity that is not conserved after all. There is not much in science that is more fundamental than that and in addition Noether’s theorem is very useful.

The picture illustrates the collision of two balls. It features mathematics demonstrating that linear momentum (mass times velocity) is preserved | Every Symmetry is Associated with a Conservation Law — If the physical laws stay the same when translated in space then linear momentum is conserved. Conservation of momentum principle in isolated system Asset id: 2319593529 by MZinchenko.

Emily Noether

Emily Noether was born into a Jewish family in Germany March 23 in 1882. She was the daughter of the mathematician Max Noether. She studied mathematics and completed her doctorate in 1907. At the time, women were largely excluded from academic positions, but she worked at the Mathematical Institute of Erlangen without pay for seven years. She eventually gained paid positions. She made huge contributions to abstract algebra, calculus of variations, topology and other mathematical fields.

Her most important contributions are the Noether’s theorems, the first one described here. When Hitler came to power in 1933, she had to flee Germany. She got a position as a professor at Bryn Mawr in 1933. She died in 1935.

Black and white photo of Emily Noether wearing a white shirt, a darker skirt and a black bowtie. — Emily Noether in 1910. Unknown author Unknown author Publisher: Mathematical Association of America [3], Brooklyn Museum [4], Agnes Scott College [5], [6], Public domain, via Wikimedia Commons.

Concluding Summary

Noether’s Theorem changes how we view the Universe and the laws of physics. For example, the conservation of energy is not just something we empirically discovered. It follows mathematically from physical laws not changing by time. It represents a paradigm shift in science that arguably is as important as quantum mechanics or relativity and yet very few people have heard of it. I find that quite shocking.