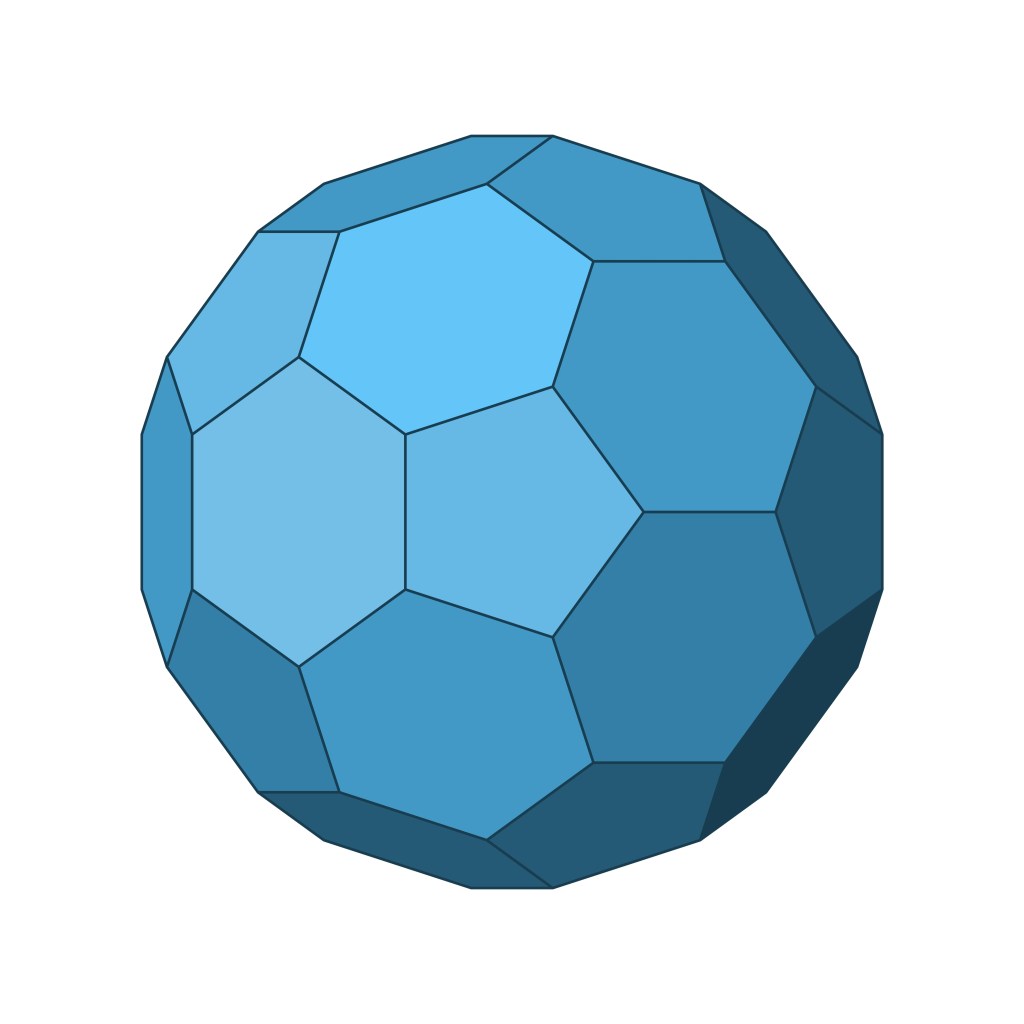
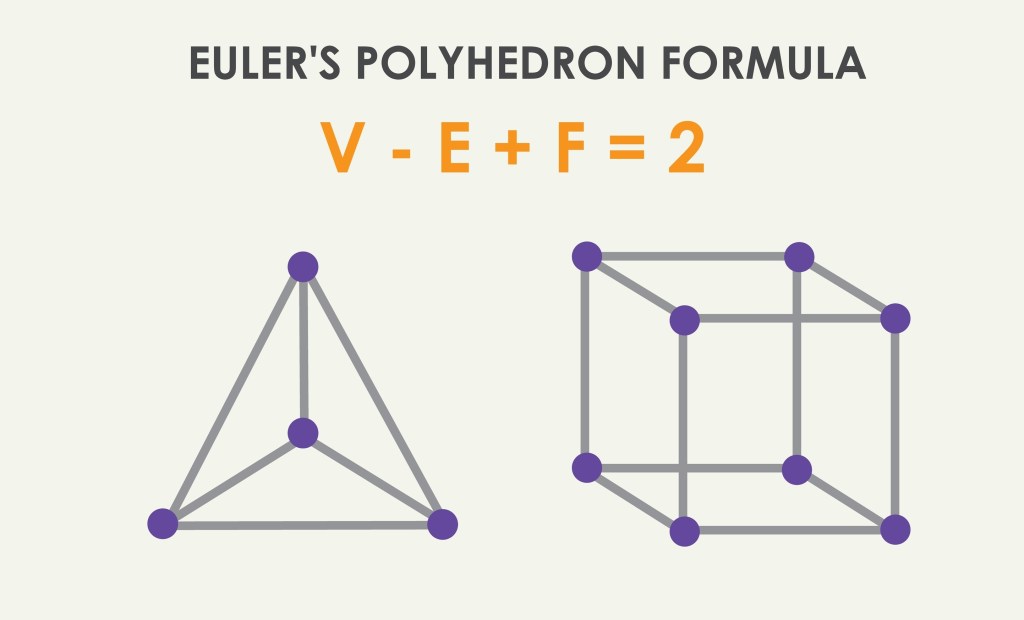
Super fact 64 : V – E + F = 2 is true for all convex polyhedra, where V is the number of vertices (corners), E is the number of edges, and F is the number of faces of a convex polyhedron. This is called Euler’s formula for polyhedra.
Convex polyhedra are polyhedra without holes, or it has no internal angles larger than 180 degrees. To express that exactly; A convex polyhedron is a three-dimensional solid with flat polygonal faces where a line segment connecting any two points on its surface or interior remains entirely within the solid. I can add that convex polyhedra consists of convex polygons as their faces. All its faces are convex polygons.

It is easy to understand that there are an infinite number of convex polyhedra. All pyramids (with convex polygons for bottoms) are convex polyhedra whether the bottom is a square/rectangle, or a convex pentagon, hexagon, heptagon, octagon, or any kind of convex polygon, even with trillions.
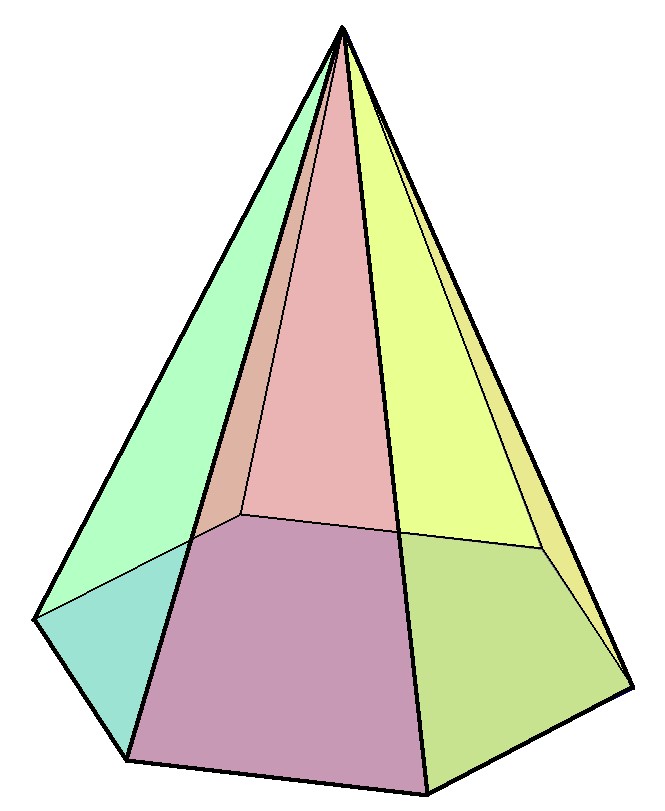
Examples of convex polyhedra are cubes, boxes, a tetrahedron, pyramids of various sorts, an octahedron, dodecahedron, icosahedron, but there are infinitely many.
As an example, take a cube (like a dice). It has six faces (F = 6), eight vertices (corners V = 8), and 12 edges (V – E + F = 2 or 8 – 12 + 6 = 2). A tetrahedron has four faces (F = 4), four vertices (V =4), and six edges (E = 6) (V – E + F = 2 or 4 – 6 + 4 = 2). A pyramid (with a square bottom) has five faces (F = 5), five vertices (V = 5) and eight edges (E = 8) (V – E + F = 2 or 5 – 8 + 5 = 2). An octahedron has eight faces (F = 8), and six vertices (V = 6), and twelve edges (E = 12) (V – E + F = 2 or 6 – 12 + 8 = 2). A dodecahedron has twelve faces (F = 12), and twenty vertices (V = 20), and thirty edges (E = 30) (V – E + F = 2 or 20 – 30 + 12 = 2). An icosahedron has twenty faces (F = 20), and twelve vertices (V = 20), and thirty edges (E = 30) (V – E + F = 2 or 12 – 30 + 20 = 2). Euler’s Polyhedral Formula works for all of them and for all the infinite number of convex polyhedra that exists.

I consider this a super fact because it is quite amazing and surprising that the number of faces, vertices, and edges follow the same formula for all convex polyhedra. At least it is surprising if you haven’t seen it before. I should say that Leonhard Euler’s most celebrated discovery is probably his discovery of the Euler Number and the associated Euler’s Formula.
More Polyhedra Examples
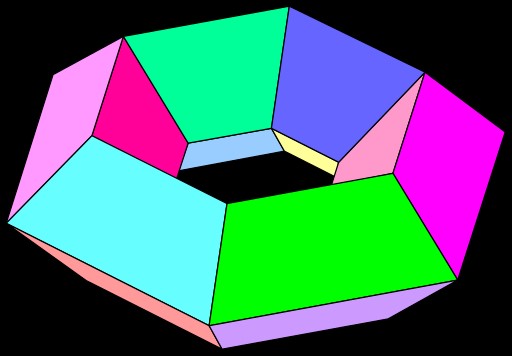
The three first examples below are convex polyhedra so Euler’s Polyhedral Formula apply. The last two examples are not so Euler’s Polyhedral Formula does not apply.