Super fact 58 : In relativity, time is considered the fourth dimension, inseparable from the three spatial dimensions to form a four-dimensional continuum called spacetime. Adding time as a fourth dimension, not (x, y, z), but (x, y, z, t), results in spacetime measurements called spacetime intervals that all observers can agree on.
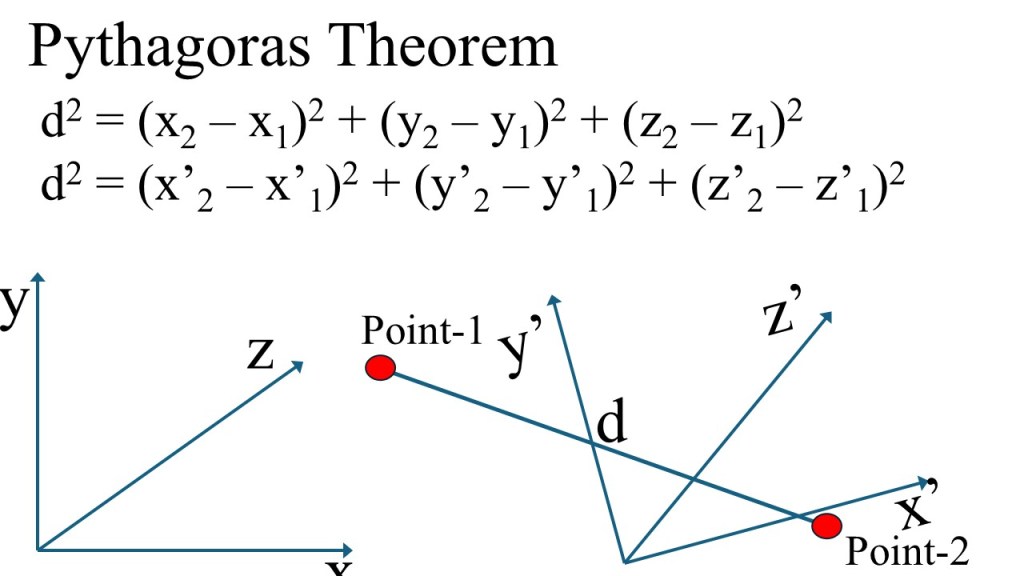
Before relativity the distance between two points was the same for all observers. The distance between points is calculated using the Pythagorean theorem: (d^{2}=x^{2}+y^{2}+z^{2}). You calculate the distance between two end points in a coordinate system using Pythagoras theorem because the points make right angled triangles along the x-axis, y-axis and z-axis. See the picture below.

Let say you add another coordinate system (x’, y’, z’). The new coordinate system could be translated and rotated compared to the first one. The values of (x, y, z) and (x’, y’, z’) would be different and yet the distance between point-1 and point-2 would be the same. Well as long as you don’t change units, like using meters in one coordinate system and feet in the other. The distance between the points would be a so-called invariant. Now imagine that you forgot to include one coordinate in Pythagoras theorem, for example, y and y’ or x and x’, then your calculation for the distance would be different for the two coordinate systems. We need all coordinates, or all dimensions. See the picture below.
In relativity the length of objects, as well as the time between events is relative and varies from observer to observer. In other words, distance and time varies from coordinate system to coordinate system. However, if you add time to the three space dimensions and calculate the distance between events using the Pythagorean theorem for intervals (between two events): or (s^{2}= x^{2}+y^{2}+z^{2} – t^{2}) or (where the ‘t’ represents time in appropriate units), then the difference between different observers vanish. The interval is the same for all observers. It is a so-called invariant. The formula for the spacetime interval comes in a few different forms. One for distance like intervals (space distance bigger than time) (s^{2}= x^{2}+y^{2}+z^{2} – t^{2}), and one for time like intervals (time is bigger than the space distance) (s^{2}= t^{2} – (x^{2}+y^{2}+z^{2})). There is also one that includes the imaginary number (s^{2}= x^{2}+y^{2}+z^{2} + (it)^{2}). See below.

The interval concept was developed, not by Einstein, but by Hermann Minkowski (a few years after special relativity) and is often referred to as Minkowski space. Time is like a space coordinate but the opposite signs in the equation make it different. Based on articles I found it appears that the opposite signs (minus vs. plus) means that you cannot move “backwards” in time as you can in a space dimension.
I admit that this is a very abstract super fact, but it basically means that if you add time as an extra coordinate to the three space coordinates x, y, z you get something, the spacetime interval, that everyone regardless of speed, orientation, etc., agrees on, despite relativistic length contraction and despite time dilation and non-simultaneity.
Time Expressed in Appropriate Units
I would also like to explain what I mean by (where the ‘t’ represents time in appropriate units), as I stated in the above. For physical formulas to work they need to be expressed in consistent units. For example, you can’t use kilometers for the coordinate x, and miles for coordinate y, not without adding a constant to adjust for it. For the formula (s^{2}=x^{2}+y^{2}+z^{2}-t^{2}) to work you need to express time in a unit that corresponds the time light travels in one meter if x, y and z are expressed in meters. If you express x, y, and z in meters and express time in seconds you must adjust the formula with the constant c = 299,792,458, the speed of light in meters per second, so you get (s^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}). See the picture below.

Time Like Space Intervals
The formula for time like intervals is typically used for the situation where the time component is larger than the space component, which also means that it is possible to physically travel between the two events forming the space interval. As you can guess, that is a pretty normal situation. Let’s say you are watching TV and having a pizza. Your sofa is your coordinate system. You turn on the TV and 100 seconds later you move 2 meters to get a slice of pizza. Let’s calculate the spacetime distance between those two events.
The space component is easy, that’s 2 meters. However, if we express time in the time it takes light (in vacuum) to travel one meter we get 100 times 299,792,458. If you express time in seconds, you adjust it using the constant c = 299,792,458, and again you multiply 100 with 299,792,458, which is 29,979,245,800. So, the distance in time is almost 15 billion times larger. You really did not move far in space, but you moved very far in time. Now ask yourself. Are you spending your time well?
The Minus in Front of the Time Coordinate
There is one obvious difference between time and the space coordinates. In a coordinate system you can walk forward, along let’s say, the x-axis and then walk back the same way. You can walk back and forth as many times as you want, no problem, but you cannot do that with time. Time may be a space-time coordinate, but it is different from the other three coordinates in that way, and that’s where the opposite signs in the formula for the space-time interval comes in. This is beyond the scope of this super fact blog post, but you can read more about this here and here.
Other Relativity Related Superfacts
- The Speed of Light In Vacuum Is a Universal Constant
- Two events may be simultaneous for some but not for others
- GPS uses relativity for accuracy
- Time Dilation Goes Both Ways
- The Pole-Barn Paradox and Solution
