The Euler Number Math Magic

Super fact 53 : The Euler number denoted e, is an irrational number, which like the number pi is extremely important in mathematics. In addition, the relationship between the Euler number and pi; seemingly unrelated numbers, is quite amazing, especially if you throw the imaginary number: i = square root of -1 into the mix. Euler’s formula e^ix = cos(x) + isin(x), where x is degrees expressed in radians, is mind blowing to say the least. Radians means that 180 degrees is replaced by pi, and 90 degrees is replaced by pi/2, etc. A simpler special case, but equally amazing is Euler’s identity e^ix = -1, or e^ix + 1 =0. This is amazing math assuming you understand it.

As I said all this is amazing, mind blowing if you will, if you understand it, which is why I will try to explain it. Why I consider this a super fact is because when you first encounter the Euler number and the Euler formula, and you somewhat understand what it means, it is likely to be a mind-blowing experience. Those among you who have studied higher math, AP math classes in high school, or college level math are probably familiar with what I am about to describe, so your mind may not be blown. By the way you pronounce Euler like “Oiler”.

Euler’s Number and Pi Two Irrational Numbers

Pi is the number you get when you divide the distance around a circle (the circumference) by the distance across the middle (the diameter). The Euler number is a bit more complicated to explain. I will do that next. Both pi and the Euler number are irrational numbers, which means that when written as a decimal, the number neither terminates nor repeats. As I mentioned, both pi and the Euler number are extremely important numbers in math. Perhaps the Euler should have its own day, just like pi has its own day (March 14). Maybe we should start celebrating Euler number day on February 7.

Exponents

Before I explain what, the Euler number is, I need to explain what an exponent is. If you multiply a number by itself x number of times, then x is the exponent. If you multiply two by itself four times 2*2*2*2, called 2 raised to 4, then 4 is the exponent. By the way the answer is 2^4 = 16 (called 2 raised to 4 is 16). I hope the illustration below will explain it.

And finally, before explaining what the Euler number is I should also mention what a factorial is. The factorial of a number is the product of all positive integers less than or equal to that number. The factorial of 5 is denoted 5! and is 1*2*3*4*5 = 120. Also, the factorial of 0 or 0! = 1 (per definition).

Definition of the Euler Number

One more thing I need to explain before I go ahead with the definition for the Euler number is what is meant by allowing a number n in a formula to go towards infinity (limit –> infinity). Let’s say you have a formula that contains the number n. If the value of the formula does not change much as n becomes very large than it might be approaching a specific number as n approaches infinity. You say that it approaches a limit. I am trying to illustrate this in the picture below.

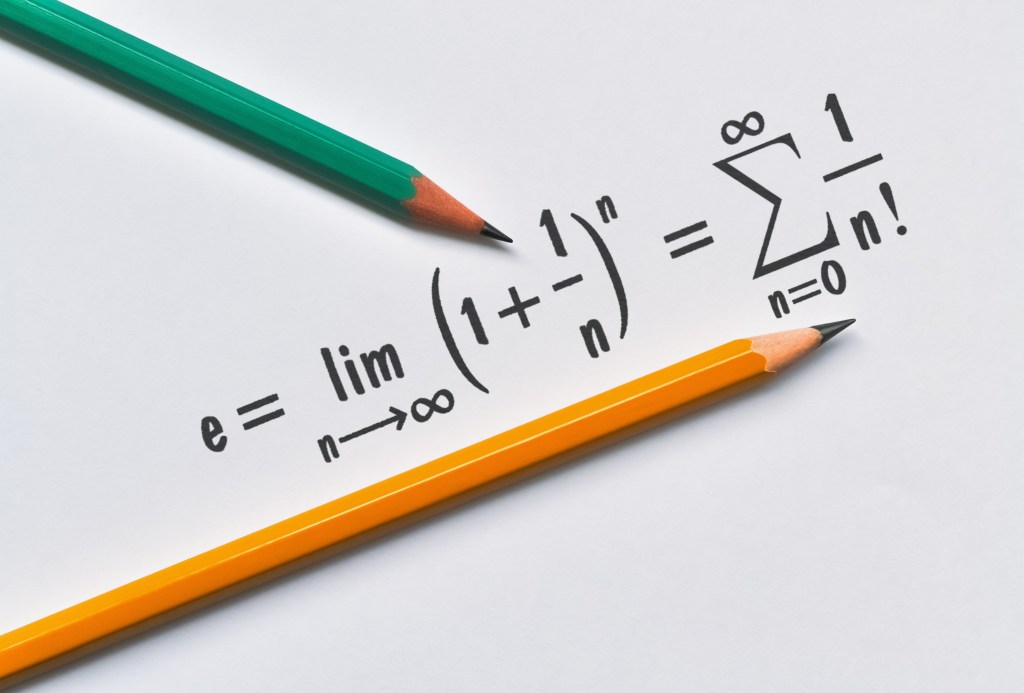
Euler’s Number in Calculus

As I mentioned, Euler’s number shows up in mathematics in a lot of places. It is an extremely useful number with some amazing properties and that includes calculus. However, explaining functions and calculus may be going a bit too far, so I am just going to simply state that the derivate of e^x is just e^x and the indefinite integral, or the anti-derivative of e^x is e^x. In other words, differentiation / integration does not change this function. It also means that the slope of the curve is the same as the curve itself. Among all the infinite number of functions this is only true for e^x.

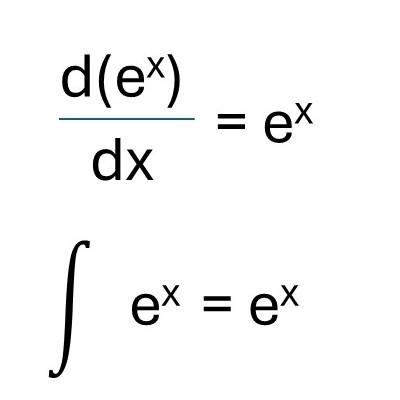
Trigonometric Functions

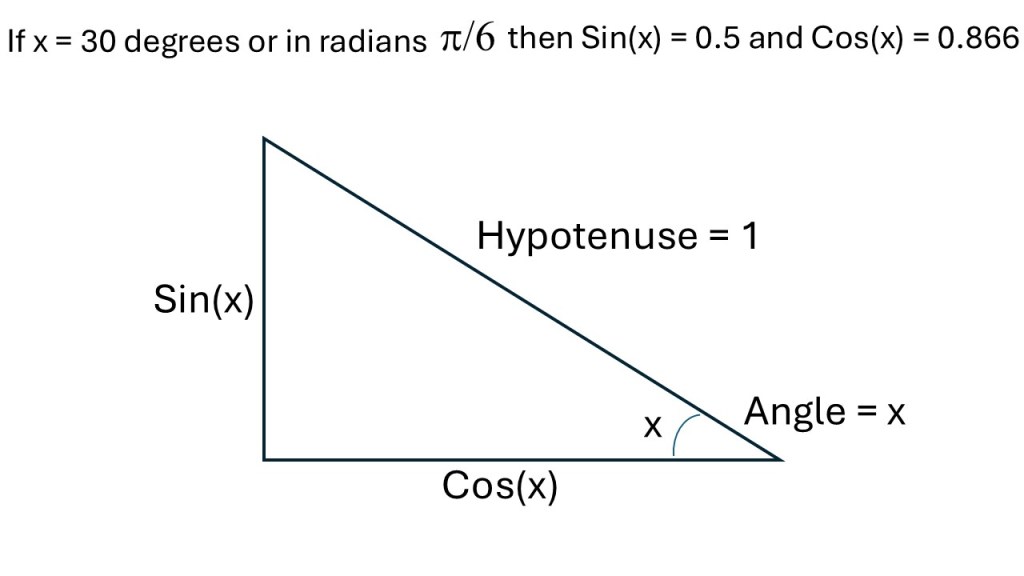
Next, I would like to launch into Euler’s formula. However, before I do that, I need to explain what trigonometric functions and imaginary numbers are. The trigonometric function sin(x) is the ratio of the length of the side opposite to a given angle to the length of the hypotenuse. In other words, if the hypotenuse is equal to 1, then sin(x) is the length of the opposite side to the given angle. The trigonometric function cos(x) is the ratio of the side of the triangle adjacent to the angle divided by the hypotenuse. In other words, if the hypotenuse is equal to 1, then cos(x) is the length of the adjacent side to the given angle.

Sin and cos are always between 1 and -1. ‘x’ is often expressed in degrees going from 0 to 360 (or 0 to 90 in a right-angled triangle). However, there is another way to express angles in triangles and that is radians. In this case the number pi corresponds to 180 degrees, pi/2 corresponds to 90 degrees, pi/4 corresponds to 45 degrees, etc. Euler’s formula uses trigonometric functions, but it only works if you use pi instead of degrees. Pi and Euler’s number have a special relationship. Sin and cos are illustrated in the picture below.

Imaginary Numbers

The last thing I need to explain before demonstrating Euler’s formula is imaginary numbers. The square root of a number is another number that, when multiplied by itself, equals the original number. For example, the square root of 4 is 2, because 2 * 2 = 4. The square root of 9 is 3, because 3 * 3 = 9. As long as you deal with real numbers, square roots must be positive numbers because you cannot multiply two numbers and get a negative number. -2 * -2 is 4, not -4.

However, that did not stop some mathematicians from making up a square root that was negative. This imaginary number is the square root of -1 and is referred to as i, yes just i, for imaginary. So, what’s the point of making up numbers that can’t exist? Well, it turned out to be quite useful and you can manipulate imaginary numbers to result in real numbers. For example, if you multiply the imaginary number i by itself i*i you get -1. If you multiply i by itself four times, in other words i^4, or i raised to 4, you get 1. Even more impressively, i raised to i, or i^i, is a real number. i^i = 0.207879… This is illustrated in the picture below.

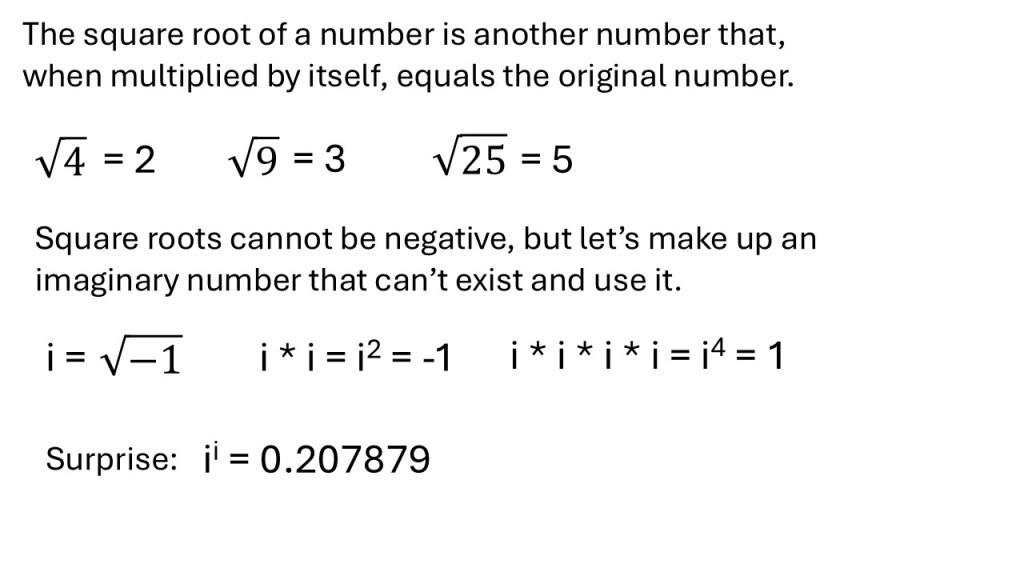
Eulers Formula

Without giving the proof, or any detailed explanations, below is Euler’s identity and Euler’s Formula (e^ix = cos(x) + isin(x)). Notice the mix of Euler’s number, pi, the trigonometric functions using radians (based on pi), and the imaginary number. Well, likely mind-blown, if you have not seen it already and you understood this post up to here.

If you want to see how you prove Euler’s Formula check out this youTube video.

If you want to learn more about the importance of Euler’s number in sommon and useful mathematics, check out this youTube video.

---

---

To see the other Super Facts click here