This is not a super fact post but another kind of fact-oriented post. It is a book review for a book that I find interesting, Relativity: The Special and the General Theory by Albert Einstein. Yes, the book was written by Albert Einstein in 1916 and translated into English in 1920. It is written for laymen, average readers, and despite being more than 100 years old (well this reprint is from 1995) it does not feel outdated.
I should say that I wrote my review decades ago and Amazon has hidden about 900 of the oldest reviews including mine. So, you can no longer find it. Luckily, I still had it, but I cannot provide a link to it. The book comes in formats, hardcover (2024), paperback (1995), Kindle (2014), Audio (2009). I bought the paperback version.
- Publisher : Independently published (July 29, 2024), ASIN : B0DBQVVJVQ, ISBN-13 : 979-8334454118, 109 pages, item weight : 7.8 ounces, dimensions : 6 x 0.47 x 9 inches, Translator : Robert W. Lawson, it costs $12.33 on US Amazon. Click here to order it from Amazon.com.
- Paperback – Publisher : Crown (June 6, 1995), ASIN : 0517884410, ISBN-13 : 978-0517884416, 208 pages, item weight : 8 ounces, dimensions : 5.2 x 0.5 x 8 inches, it costs $7.89 on US Amazon. Click here to order it from Amazon.com.
- Kindle – Publisher : Amazon Kindle Direct Publishing (February 23, 2014), ASIN : B004M8S53U, 126 pages, it costs $0.99 on US Amazon. Click here to order it from Amazon.com.
- Audiobook – Publisher : HighBridge, a division of Recorded Books (November 14, 2009), ASIN : B002XGLDAA, Listening Length : 2 hours and 14 minutes, it costs $12.09 on US Amazon. Click here to order it from Amazon.com.

Amazon’s Description of Relativity by Albert Einstein
This book was originally written in German by Albert Einstein in 1916 and later translated to English by Robert W. Lawson in 1920. In Einstein’s own words, “The present book is intended, as far as possible, to give an exact insight into the theory of Relativity to those readers who, from a general scientific and philosophical point of view, are interested in the theory, but who are not conversant with the mathematical apparatus of theoretical physics. It is an easy-to-understand collection of the ideas of one of the greatest scientists of the twentieth century including the idea he is most known for, the theory of relativity.
Redesigned inside and out to have a fresh, appealing look, this new edition of a classic Crown Trade Paperback is a collection of Einstein’s own popular writings on his work and describes the meaning of his main theories in a way virtually everyone can understand.
Below is my review for Relativity: The Special and the General Theory by Albert Einstein. First, I should mention that the book is divided into two sections, one for the Special Theory of Relativity and another for the General Theory of Relativity. In addition, there are five short appendices. The five appendices are not written for layman and require at least high school mathematics.
Relativity Explained by Einstein himself
I found it very interesting to read an explanation of the theories of relativity by the developer of those theories. However, it is important to remember that the inventors of science theories aren’t always the best ones to explain them. Isaac Newton is a prime example.
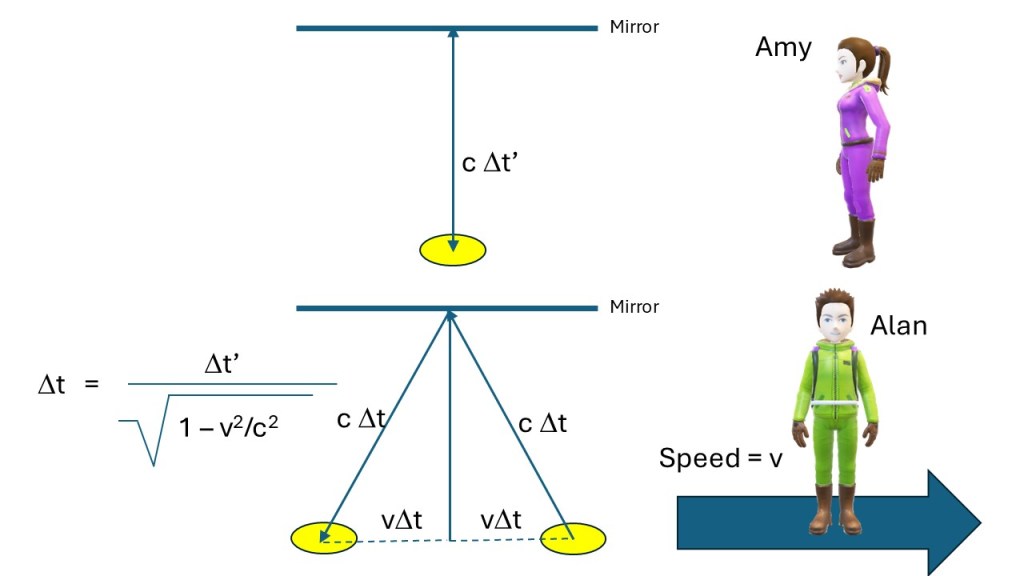
Another thing to remember is that today there are a lot of books and online graphics that use clever pedagogic techniques and visualizations to assist you in understanding these theories, and naturally this book does not contain any of that.
This book was originally written in 1916 and updated in 1920 and since then it has been reprinted/edited several times (as this book is an example of). I should say that the General Theory of Relativity had just been published so there weren’t much else out there for laymen at the time.
I’ve already read many good books on relativity, and I believe I understand special relativity pretty well, but my understanding of general relativity is partial. I did not buy this book to understand relativity. The reason I bought this book was to gain another perspective on the subject. If you just want to learn and understand relativity, I recommend Relativity Visualized by Lewis Carroll Epstein instead.
“Relativity: The Special and the General Theory” features no derivations of the formulas in relativity (except in the appendix) and no visualizations demonstrating relativistic effects and phenomena. The book is focused on the conceptual foundations of relativity and physics.
For example, what are Geometrical propositions, what does it mean to measure the length of a rod, or the time of an event, what do we mean by speed, what is simultaneity, what is the difference between what we observe and what we measure, etc? Einstein spends one and a half page explaining addition of velocities in classical-pre-relativistic kinematics (w = v + u) and what assumptions that are inherent with the approach. In that sense the book is quite philosophical, which is what I meant by “another perspective”. The book covers both the Special Theory of Relativity and the General Theory of Relativity. However, the sections on the General Theory of Relativity are quite short and very introductory.
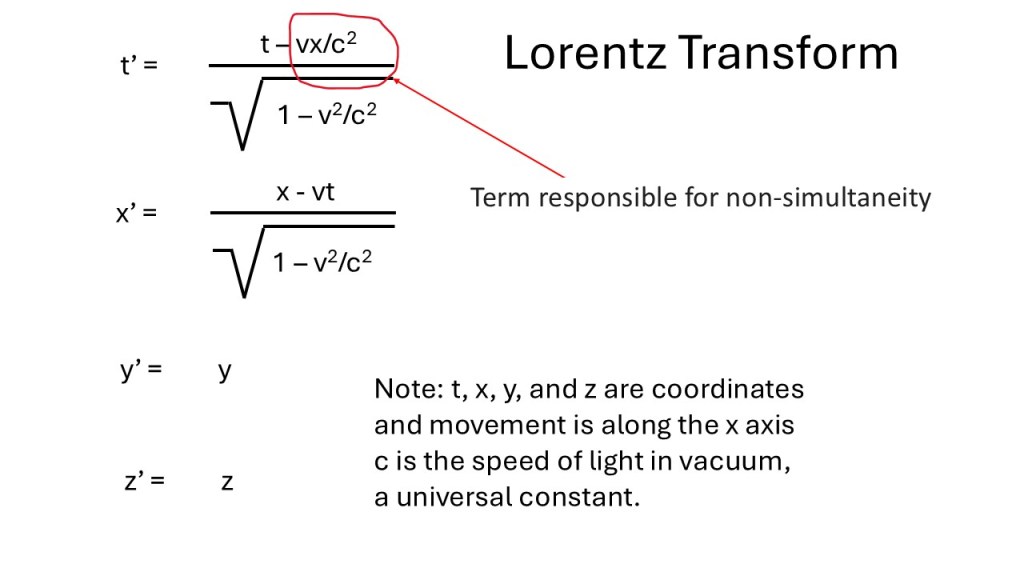
There are some issues with the book. In appendix 1 Einstein (I presume) derives the Lorentz transforms. However, it is not, in my opinion, the best derivation from a pedagogical standpoint and it also had typos in it. As far as I can tell the formula on page 50 is wrong unless what Einstein means with the “m” is “additional relative mass” and not actual “mass” as stated.
The book features an addition written in 1920 where he is discussing an ad hoc modification to his theory that he had previously made but it turned out to be unnecessary (related to cosmology). The language is also very old fashioned. On the other hand, this kind of stuff makes you feel as if you travel back in time to when the theories of relativity were being churned out.
I don’t recommend the book for learning the theories of relativity but overall I liked the book. It focuses very much on basic concepts and near philosophical aspects of time, space and relativity. The book presents a valuable perspective if you already understand what the theories of relativity are about.

Other Relativity Related Posts
- Book Review : Relativity Visualized by Lewis Carroll Epstein.
- Book Review : The Special Theory of Relativity by David Bohm.
- The Speed of Light In Vacuum Is a Universal Constant.
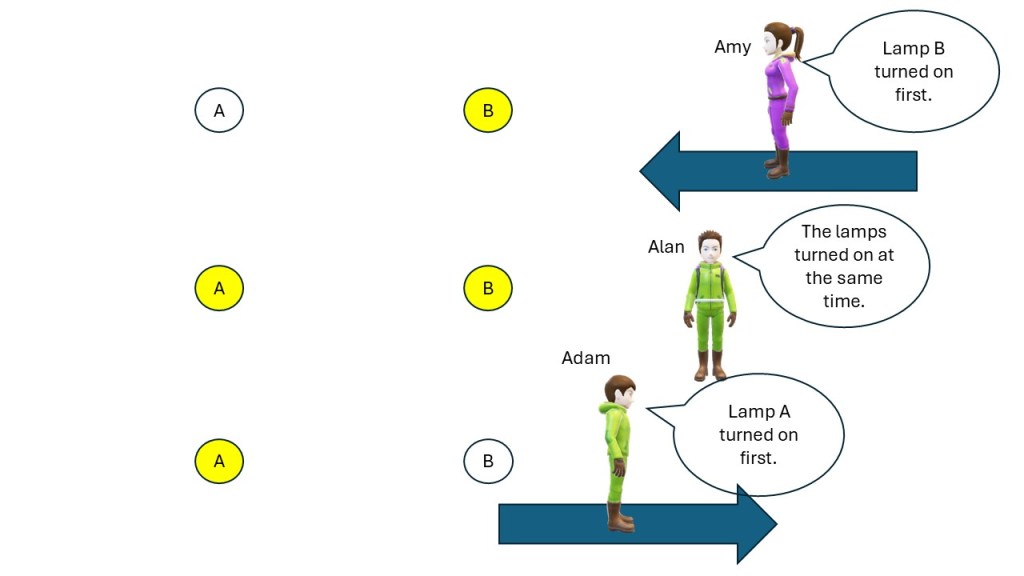
- Two events may be simultaneous for some but not for others.
- Time Dilation Goes Both Ways.
- The Pole-Barn Paradox and Solution.
- What is Time.