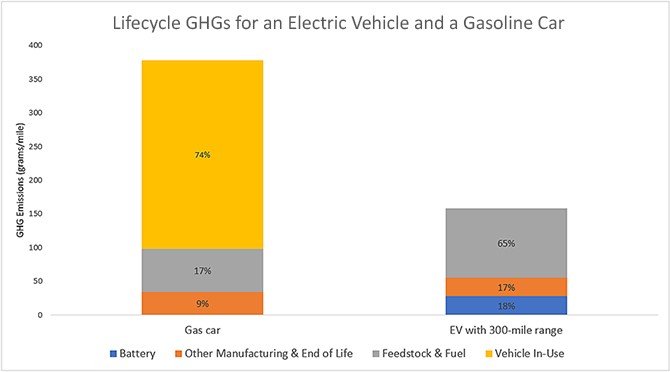
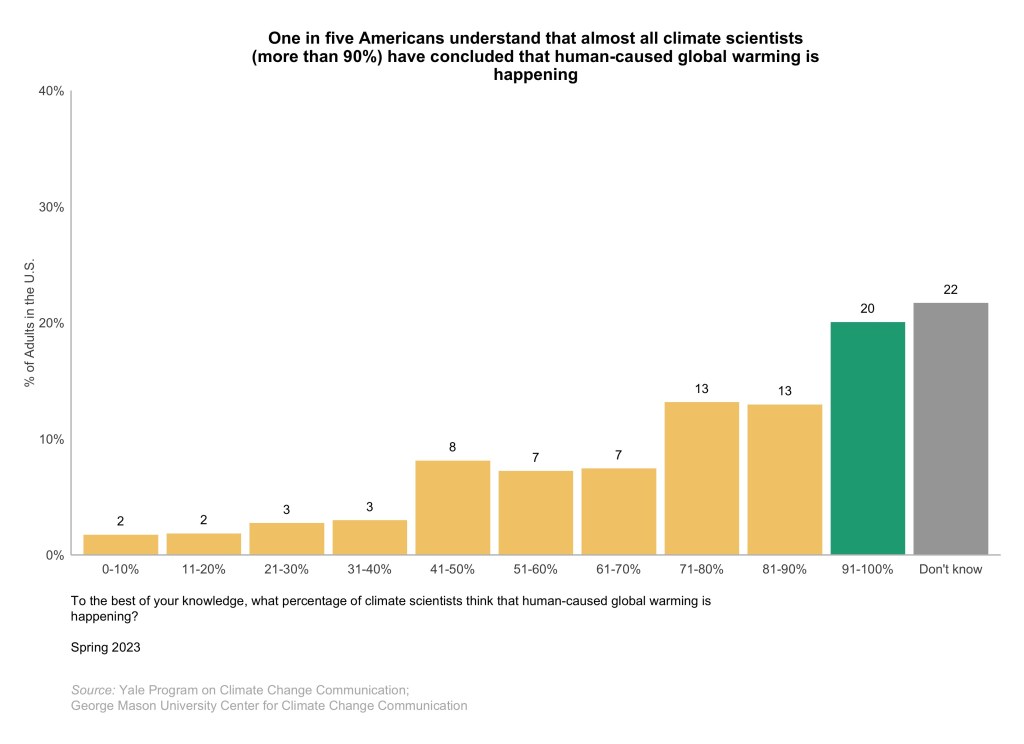
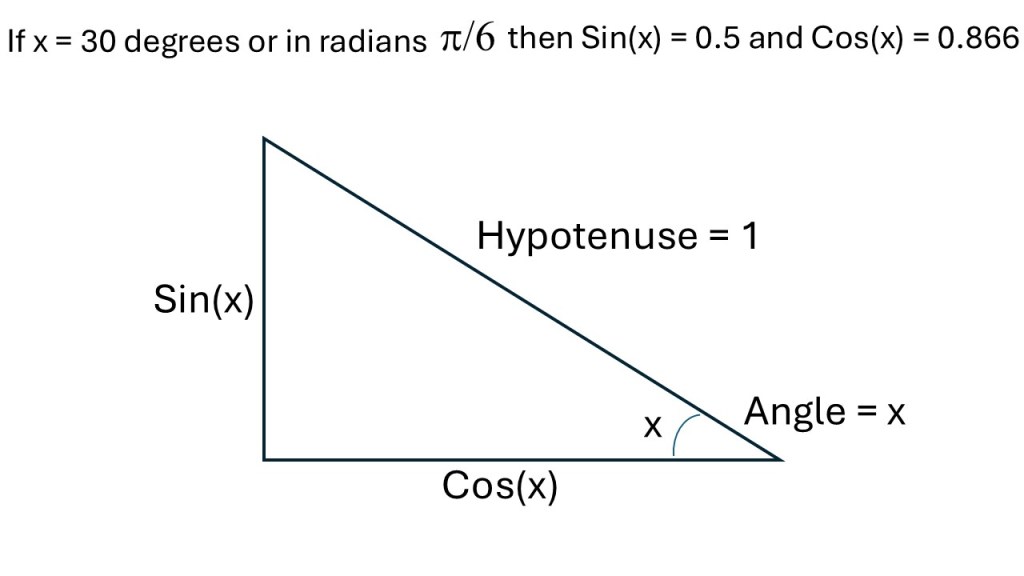
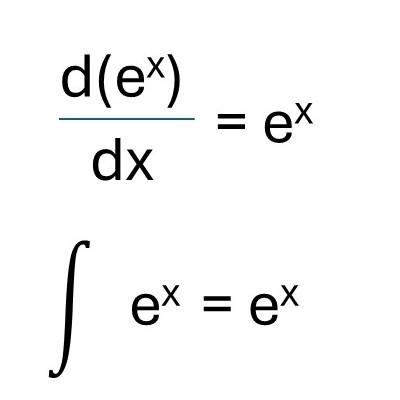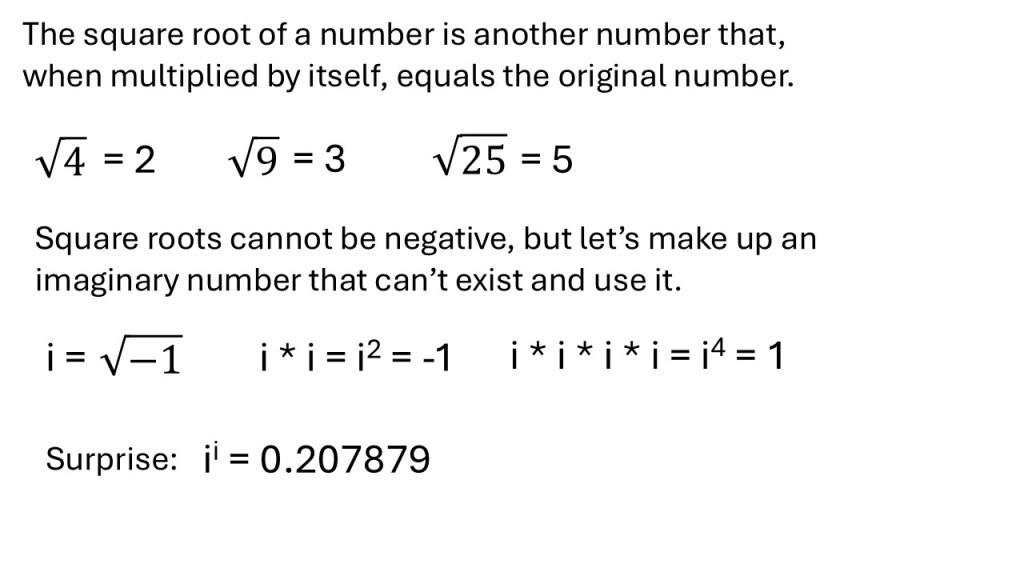Math & Logic – Super Facts

Conic Sections are the Shapes that Shape Our World

Super fact 80 : A conic section is a shape formed by slicing a cone with a plane. There are four such shapes, circle, ellipse, parabola, and hyperbola. The conic sections universally describe motion under gravity. The orbits of planets around their stars are circles or ellipses, comets fly around space in elliptical orbits, or parabolic or hyperbolic paths. Objects thrown up in the air follow parabolic paths. They are the basis for a huge amount of engineering applications.

Esther’s writing prompt: January 21 : Shapes

Click here or here to join in.

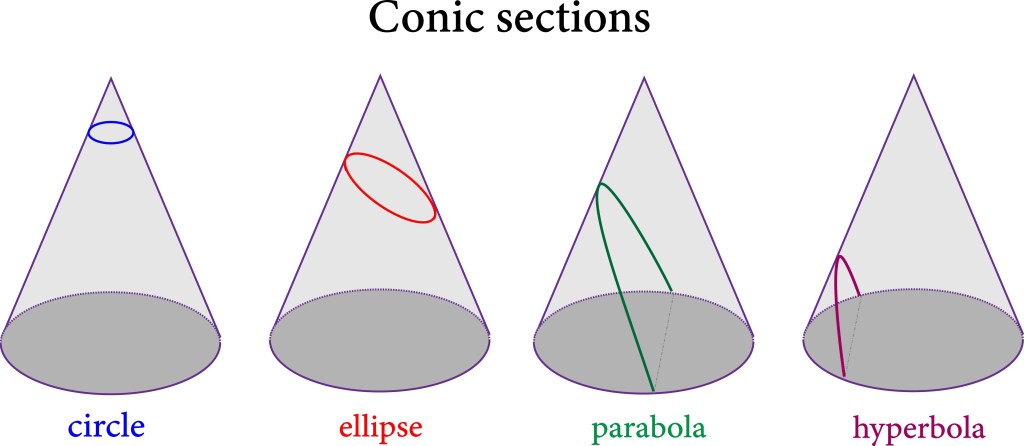
Four cones each shown with a plane section forming a specific conic section. | Conic Sections are the Shapes that Shape Our World — Types of conic sections : circle , ellipse , parabola , hyperbola Shutterstock Asset id: 2377159367 by ProfDesigner

The four conic sections, circle, ellipse, parabola and hyperbola are fundamental and very useful shapes in mathematics, physics and engineering. Well, a circle is a special case of an ellipse, so it is really only three conic sections. The motion of the planets and other stellar objects are described by the conic shapes. Isaac Newton derived his law of gravitation from Kepler’s laws, which describe planetary orbits as ellipses.

The conic sections are all described by second degree equations (quadratic equations) and are in that sense the simplest shapes aside from points and lines. It is important to understand that there is an infinite amount of shapes that are almost conic sections and look like conic sections, but it is the exact mathematical properties of the four conic sections that make them so common in physics, mathematics, nature and engineering.

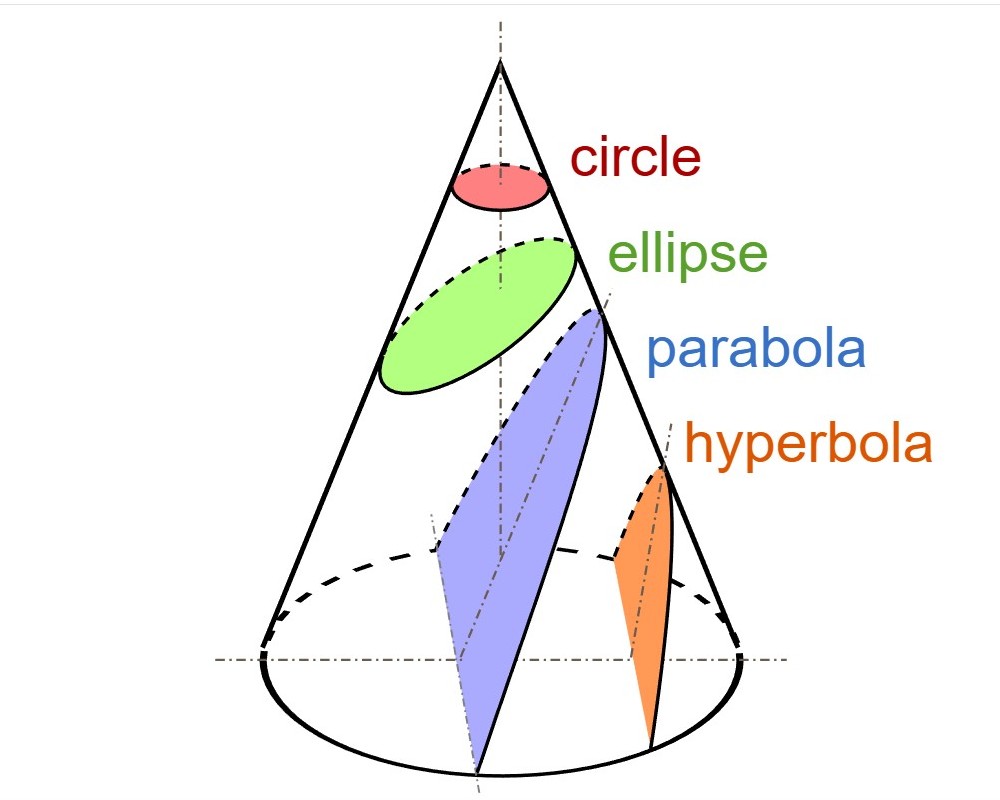
The picture shows a cone with four planes slicing the cone in four ways. The resulting shapes are circle (red), ellipse (green), parabola (blue), hyperbola (orange). — The black boundaries of the colored regions are conic sections. Not shown is the other half of the hyperbola, which is on the unshown other half of the double cone. by Magister Mathematicae, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18556148

It may not come as a surprise that the circle is a fundamental and important shape, but I believe that the fact that the other conic sections are also fundamental in mathematics, physics and engineering come as a surprise to people outside of the STEM fields. It is a true and an important fact regarding how our world works.

Conic Sections

As mentioned, the conic sections are fundamental shapes that appear in a lot of places in STEM. Below are a few examples.

Parabola

A parabola is formed when a plane cuts a cone, so the plane is parallel to a side of the cone. Parabolas are shapes that are roughly U-shaped and described by the equation y = x^2 or more generally by y = ax^2 + bx + c. Parabolas have a so called focus point. See the picture below. If you throw a ball, or any object, up in the air its trajectory will be a parabola (ignoring distortions caused by friction and wind). I should say the parabola you get in this case is upside down. The parabola is important when you design any kind of projectile.

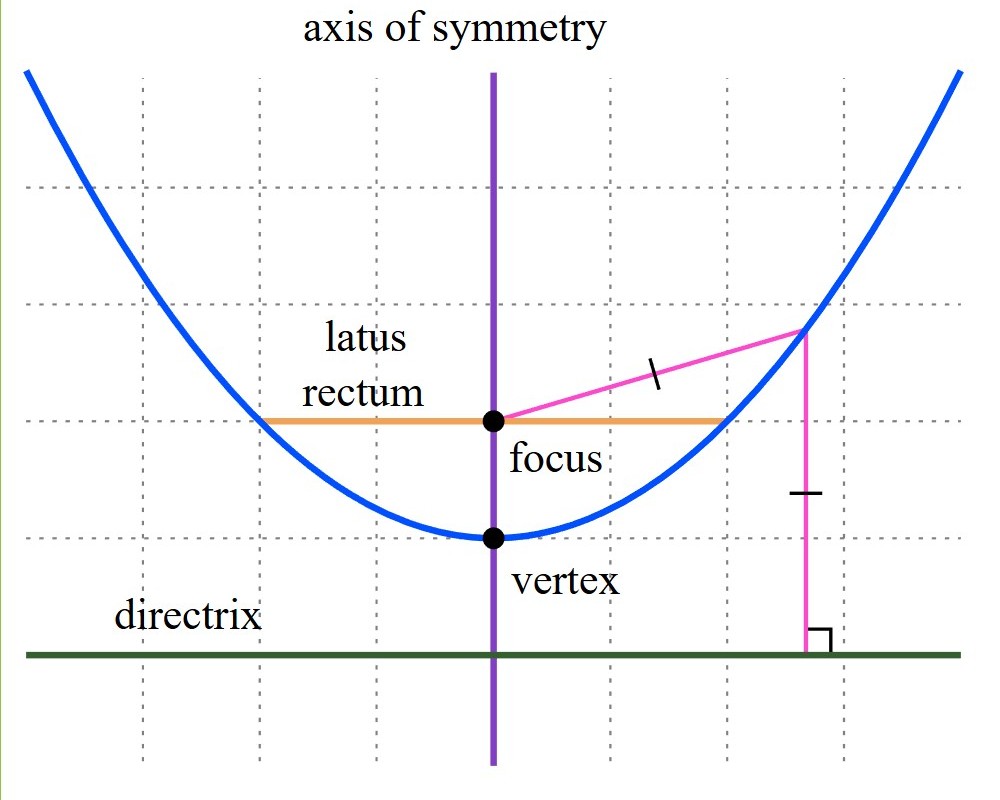
U-shaped parabola with the focus shown. The pciture has an x-axis and a y-axis. — Part of a parabola (blue), with various features (other colours). The complete parabola has no endpoints. In this orientation, it extends infinitely to the left, right, and upward. Picture is from Wikipedia Melikamp, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons.

Antennas shaped like parabolas (in 3D) will direct incoming radiation and waves towards their focus point. If the surface is reflective a light located at the focus point will reflect to create a straight beam. Parabolas are used for radio telescopes, satellite dishes, car headlights, flashlights, solar cookers, solar power plants, water fountains, suspension bridges, business modelling and thousands of engineering applications. Parabolas like circles and the other conic sections shape our modern world (pun intended).

A parabola dish with equipment located at the focus. — Würzburg-Riese radar built by Germany in WW2 had a 7.4 meter (24 foot) dish. From this page. Alan Wilson from Stilton, Peterborough, Cambs, UK, CC BY-SA 2.0 https://creativecommons.org/licenses/by-sa/2.0, via Wikimedia Commons

Ellipse and circle

As mentioned, a circle and an ellipse are conic sections formed by intersecting a plane with a cone. You get a circle when the cuts perpendicular to the cone’s axis (see pictures above) and an ellipse form when the plane intersects the cone at a slant but not slanted so much that it becomes a parabola or a hyperbola. An alternative for an ellipse is that the sum of the distances from any point on the curve to two fixed points (called the foci) is a constant. See the picture below. The two definitions are identical. For a circle the two foci are merged into one point at the center.

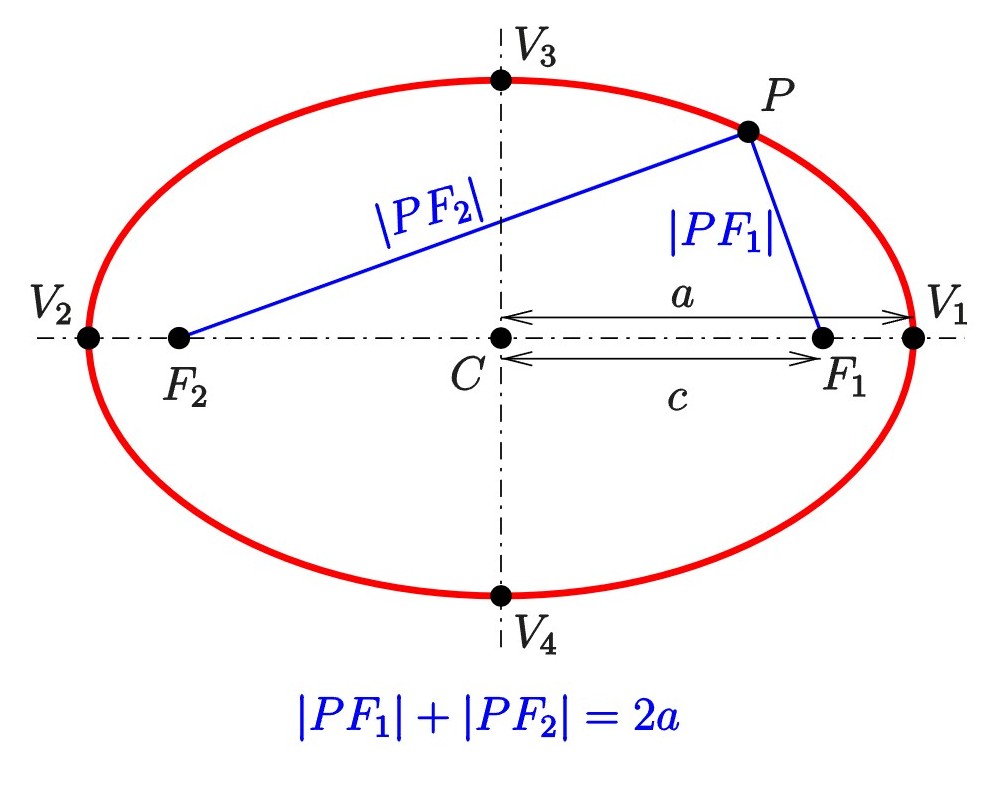
The picture shows an ellipse and its two foci points. From the foci points there are lines going to a point P on the ellipse. The length of the two lines are added together and is the sum “2a” no matter where on the ellipse the point P is located. | Conic Sections are the Shapes that Shape Our World — Ellipse: definition by sum of distances to foci. Ag2gaeh, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

There are a lot of real world examples of ellipses. Planets orbit the Sun in elliptical paths. The sun is in one of the foci points. The orbits of other stellar objects and satellites are also elliptical. Charged particles follow elliptical paths within magnetic fields. Elliptical patterns are observed in the rotation of ocean currents, elliptical models and algorithms are used in medical imaging, computer science and encryption. Also whispering galleries.

Hyperbola

Comets and spacecraft that are not orbiting another body, in other words, they have enough speed to escape the gravitational pull and continue into deep space, will travel along a hyperbola. The boundary of a shockwave from a supersonic jet (a sonic boom) creates a hyperbolic curve on the ground as it moves. The intersection of two sets of concentric ripples in water makes a hyperbola. The light beam from a lamp or flashlight makes an ellipse or an hyperbola on a plane depending on the angle.

Newton’s Law of Gravitation

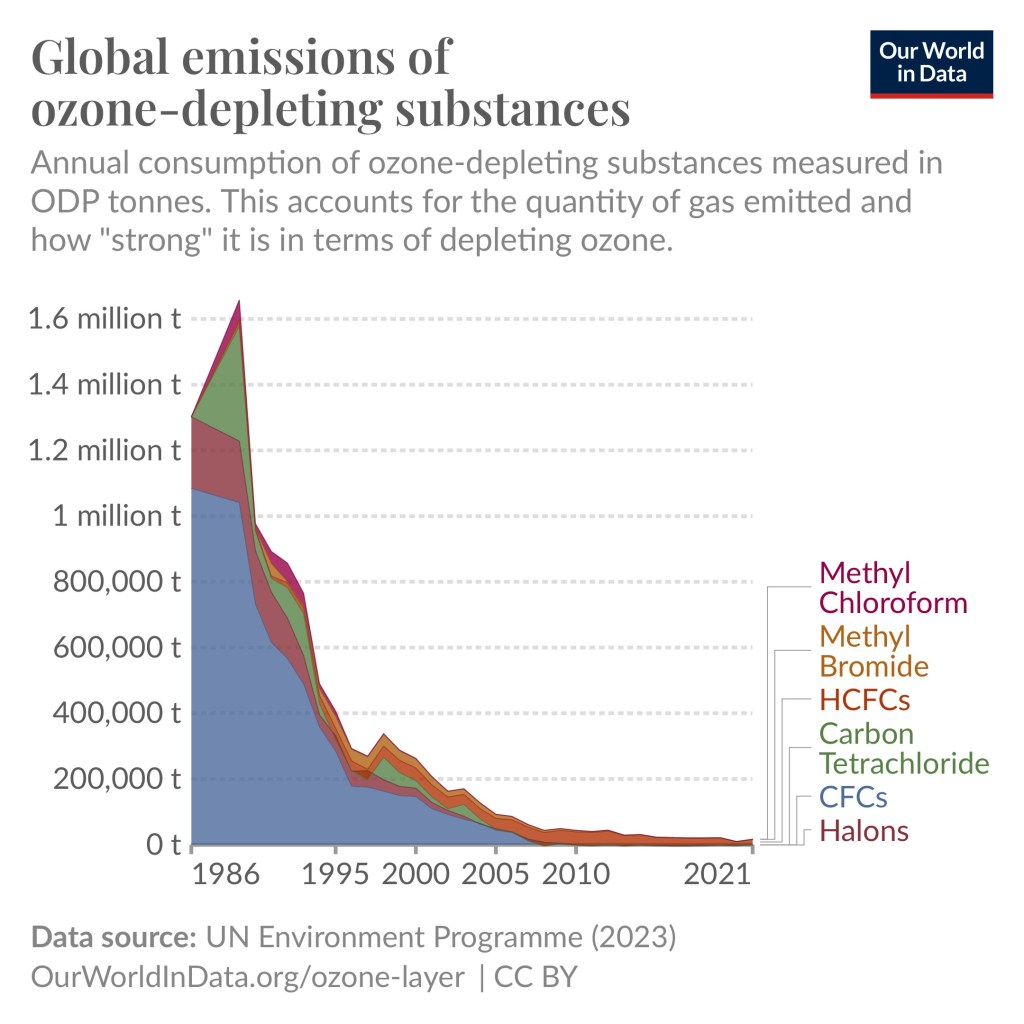
Johannes was an early 17^th century German mathematician who derived three laws that describe how planetary bodies orbit the Sun using the observational data collected by the Danish astronomer Tycho Brahe. The three laws are the following:

Planets move in elliptical orbits with the Sun as a focus.
A planet covers the same area of space in the same amount of time no matter where it is in its orbit.
A planet’s orbital period is proportional to the size of its orbit (its semi-major axis).

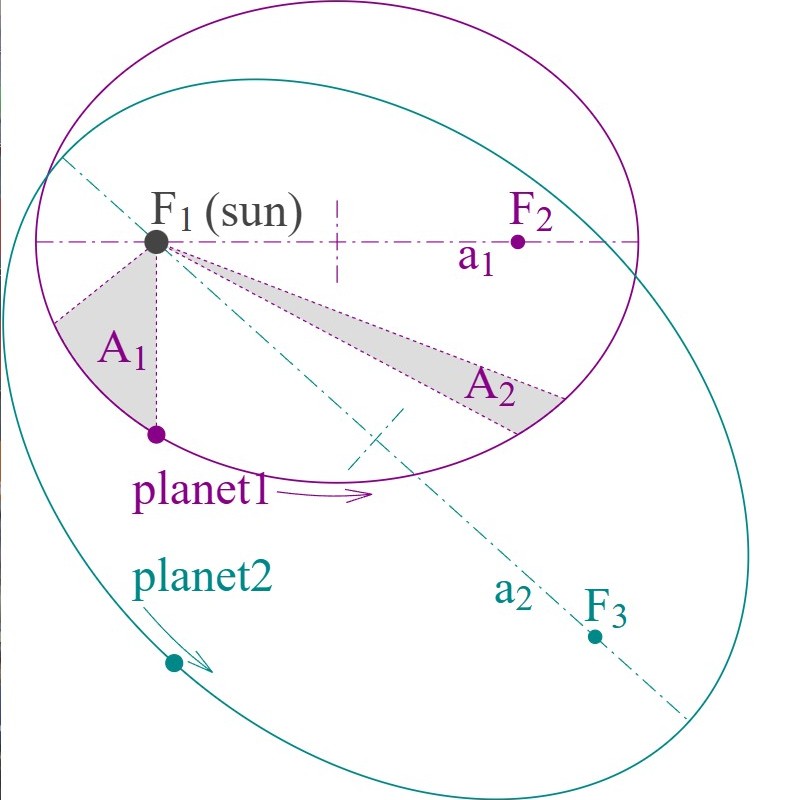
Kepler’s three laws are illustrated in a diagram for two planets. — Illustration of Kepler’s laws with two planetary orbits.
The orbits are ellipses, with foci F1 and F2 for Planet 1, and F1 and F3 for Planet 2. The Sun is at F1.
The shaded areas A1 and A2 are equal and are swept out in equal times by Planet 1’s orbit.
The ratio of Planet 1’s orbit time to Planet 2’s is (a1/a2)^3/2
Hankwang, CC BY-SA 3.0 <http://creativecommons.org/licenses/by-sa/3.0/>, via Wikimedia Commons

Later Isaac Netwon would use Kepler’s three laws to derive his law of gravity. Newton showed that an inverse-square force (gravity) directed toward the sun was necessary to explain the orbits.

My Other Responses to Esther’s Prompts

Prompt : Small : Small Microscopic Subatomic and Strings
Prompt : Kind : Leonbergers Are Kind Dogs
Prompt : Charge : Electric Charge is not the only type of Fundamental Charge
Prompt : Promises : Promises To My Dog
Prompt : Shade : A Total Solar Eclipse the Ultimate Moon Shade
Prompt : Money : Ten Money Facts
Prompt : Edge : The Edge of the Observable Universe is 46.5 billion Light Years Away
Prompt : Fish : Ten Amazing Fish Facts
Prompt : Promise : I Promise Not to Post AI Generated Comments
Prompt : Respect : Respect your Dog
Prompt : Giving : Leonbergers Giving Gifts to Pugs
Prompt : Family : Dogs Are Family
Prompt : Snow : Snow and Ice in Norrland
Prompt : Red : The Universe has a Redshift and its Increasing

To see the other Super Facts click here

Ten Selected 2025 Super Facts

I started this blog, superfactful, in August of 2024. The goal of my blog is to create a list of facts that are important, not trivia, and that are known to be true yet surprising, shocking or disputed by large segments of the public. I determine what is true by evaluating the evidence I find in reliable reputable sources and if a longstanding scientific consensus is available that certainly helps. In some cases, I have expertise in the subject myself, which also helps. Whether a fact is important and surprising or disputed is a judgment call. In some cases, there are polls to help me determine how surprising or disputed the fact is. I am trying to avoid trivia and click bait, and I am only focusing on what is true, important and mindboggling.

It is a project I hope to learn a lot from, and I hope others will also learn something from reading it. We are all drowning in misinformation, false beliefs and unsubstantiated assumptions. We often know and understand less than we think. I have been bamboozled in the past and I am pretty sure you have too. If this blog can spread a little bit of light, I am happy.

In 2024 I posted 25 super facts and in 2025 I posted 53. I am hoping to one day to have collected 200 super facts. I have also made 64 other kinds of posts on this blog such as book reviews for educational books as well as other fact related posts. Below are ten selected super facts from 2025. To read the full post click the links.

That Earth is round was well known long before Columbus

Super fact 28: That Earth is round, or spherical (or closely spherical) had been known for at least a couple of thousand years by the time Columbus set sail. Columbus did not set sail to prove that earth was round, and he knew it was round.

I’ve realized that this comes as a surprise to some. To read the post click here.

The earth globe showing the side with the Pacific Ocean. The Pacific Ocean covers most of this side. | Ten Selected 2025 Super Facts — Columbus thought earth was smaller. He did not know about the Pacific Ocean. Earth Pacific Ocean view Stock Illustration ID: 1617553012 by Matis75

EV Cars Indeed Emit Less Carbon Pollution

Super fact 29: EV Cars emit less pollution than Internal Combustion Engine, even considering manufacturing, disposal and EV Cars being charged by dirty grids.

There is a lot of misinformation about EVs including that EVs are not better for the environment. To read the post click here.

The histogram graph show that if you consider construction of facilities, manufacturing of vehicle and battery, production of fuel, vehicle operation as well as disposal the total average greenhouse gas emissions from EV cars is 52% less. — Lifecycle greenhouse gas emissions comparison of average gasoline car and 300 mile range EV. Feedstock and fuel include the generation of electricity for EVs.

Scientists Agree that Global Warming is happening and that we are the Cause

Super fact 34: Climate Scientists agree that Global Warming or if you call it Climate Change is happening, and that it is caused by us primarily because of our burning of fossil fuels. There is a long-standing scientific consensus on these two facts because the evidence is conclusive. Typically, studies show an agreement of at least 97% or 98% among climate scientists.

Polls show that most American are unaware of the consensus among climate scientists. To read the post click here.

There is almost total agreement among climate scientists that global warming, or climate change, is happening and is caused by us. To understand why, you need to know a little bit about the impressive evidence, which for all practical purposes is conclusive. Take a look at this post “Global Warming is Happening and is Caused by us”

The green graph is going up slightly starting from 46% in 2009 and ending in 58% in 2023. The black graph starts at 33% in 2009 and ends in 22% in 2023. The yellow graph starts at 2% in 2009 and ends in 2% in 2023. — The green graph corresponds to “most scientists think global warming is happening (%).” The black graph corresponds to “there is a lot of disagreement among scientists (%)”. The yellow graph corresponds to “Most scientists think global warming is NOT happening (%)”. Graph taken from the Yale Program on Climate Change Communication.

Time Dilation Goes Both Ways

Super fact 38 : If two observers are moving compared to each other both will observe the other’s time as being slower. In other words, both observers will observe the other’s clocks as ticking slower. Time slowing down is referred to as Time Dilation.

Clocks slow down as you travel at high speeds. However, the person travelling think they are standing still. It is the other person who is travelling. This is confusing. To understand it click here.

The picture shows two people Alan and Amy. Alan is on the ground. Amy is flying by Alan in a rocket speeding left. Both Alan and Amy are pointing lasers to the left. | Ten Selected 2025 Super Facts — In this picture Amy is traveling past Alan in a rocket. Both have a laser. Both measure the speed of both laser beams to be c = 299,792,458 meters per second. The speed of light is a universal constant.

Emissions of ozone-depleting gases have fallen by 99 Percent

Super fact 41 : Largely thanks to the Montreal Protocol in 1987 the emissions of ozone-depleting gases have fallen by more than 99%, 99.7% to be exact, according to Our World in Data. This has resulted in halting the expansion of the ozone holes and the reduction in emissions of ozone-depleting gases is saving millions of lives every year.

A gigantic victory for the environment that few are aware of. To read the post click here.

Gases visualized in the diagram are CFCs, Halons, HCFCs, Carbon Tetrachloride, Methyl Bromide, Methyl Chloroform. The diagram shows a peak around the end of 1980’s. — The phase out of six ozone depleting gases. Data source UN Environment Program (2023).

Sulfur dioxide pollution has fallen by 95 percent in the US

Super fact 44 : Sulfur dioxide pollution in the US has fallen by approximately 95% since the 1970s. This significant reduction is primarily due to regulations like the Clean Air Act. Global sulfur dioxide pollution has also fallen but not as much.

Another big victory for the environment that we seldom hear of. To read the post click here.

The graph shows a steep increase towards the end of the 19th century with a peak in 1973, followed by a steep decline. — US sulfur dioxide pollution since 1800. Data Source: Hoesly et al (2024) – Community Emissions Data System (CEDS). This graph is taken this page in Our World In Data. US Emissions peaked in 1973.

I should mention that by clicking this link you can visit the graph above Our World in Data and select different countries and regions and play around with the settings.

We Exploded Thousands of Nuclear Bombs

Super fact 48 : Since 1945 we have set off more than 2,000 Nuclear Bombs corresponding to a yield of an estimated 42,000 times that of the Hiroshima Bomb.

That we have exploded these many nuclear bombs was a surprise to me and perhaps to you too. To read the post click here.

Russian Tsar Bomba mushroom cloud rising high above the clouds. High quality photo realist ( 3d make ). | Ten Selected 2025 Super Facts — This is an illustration of the Tsar Bomba explosion by by mbafai Shutterstock Asset id: 2208486661. To see a photo of the actual Tsar Bomba explosion click here (it is copyrighted).

The Euler Number Math Magic

Super fact 53 : The Euler number denoted e, is an irrational number, which like the number pi is extremely important in mathematics. In addition, the relationship between the Euler number and pi; seemingly unrelated numbers, is quite amazing, especially if you throw the imaginary number: i = square root of -1 into the mix. Euler’s formula e^ix = cos(x) + isin(x), where x is degrees expressed in radians, is mind blowing to say the least. Radians means that 180 degrees is replaced by pi, and 90 degrees is replaced by pi/2, etc. A simpler special case, but equally amazing is Euler’s identity e^ix = -1, or e^ix + 1 =0. This is amazing math assuming you understand it.

One of the most amazing math facts explained. To read the post click here.

The formula e^ix + 1 =0 shown on a blue and black background. | Ten Selected 2025 Super Facts — Euler’s formula in cyber space with grid 3d illustration, Asset id: 1636161301 by Giggle2000

The Bermuda Triangle the Big Non-Mystery

Super fact 56 : The Bermuda Triangle mystery is a myth. There is not a higher risk of disappearances in the Bermuda Triangle. To be specific, disappearances do not occur in the so-called Bermuda Triangle, or Devils Triangle, with any higher frequency than in other comparable regions of the ocean. The “mystery” of the Bermuda Triangle is largely a manufactured one, perpetuated by sensationalized accounts that often misrepresent the facts and downplay the role of natural hazards like storms.

A surprise to the people who are convinced that there really is a mystery. To read the post click here.

The Bermuda triangle has one corner in Bermuda, one in Puerto Rico and one around Miami, Florida. — The Bermuda Triangle: It is approximately defined as a triangle Florida, Bermuda, and Puerto Rico. There is no exact definition. Alphaiosderivative work: -Majestic-, Public domain, via Wikimedia Commons.

Evolution is a Fact

Super fact 63 : Evolution is both a fact and a scientific theory. It is a fact that life has changed over time. This is supported by overwhelming evidence, while the theory of evolution provides a comprehensive scientific explanation for these changes, using processes like natural selection.

Yes, there are scientific facts, and that evolution is happening is an observed scientific fact. To read the post click here.

A photo of a trilobite fossil. | Ten Selected 2025 Super Facts — The fossil record is a lot more solid and much less problematic than the creationist books I have read claimed. Shutter Stock Photo ID: 1323000239 by Alizada Studios

Happy New Year to You All

To see the other Super Facts click here

Infinities Come in Different Sizes

Super fact 68 : Infinities come in different sizes. Some infinities are larger than others. In fact, it is possible to create an infinite number of different-sized infinities. Some infinities are countable and others are uncountable.

How can infinity be of different sizes? Infinity is infinity after all. Infinity is an absolute, an absolute we cannot imagine. However, at the end of the 19^th century a German mathematician by the name Georg Cantor demonstrated that there exists a variety of infinities, and some are larger than others. In fact, his theorem implies the existence of an infinity of infinities. For those who have not heard of this concept before it is surprising and yet it is true, and it is also kind of an important thing to know about mathematics. This is why I consider this a super fact.

Let me explain. Think about all natural numbers, 1, 2, 3, 4, 5, …, a billion, a quintillion, … You can keep counting forever. There are infinitely many natural numbers. Now take two natural numbers, the numbers 3 and 4. How many numbers are in between 3 and 4? Well, you have 3.5, 3.55555, 3.016893, and you have the number pi, 3.14159265358979323846, and infinitely many other numbers with infinitely many decimals. 3 and 4 are only two numbers but you have infinitely many decimal numbers, or so called real numbers, between 3 and 4. That is true for the two numbers 4 and 5 as well, and 5 and 6, and all natural numbers. Even though there are infinitely many natural numbers there are infinitely many more real numbers.

For the explanation of the mathematical proof see this article in Scientific American. This article explains why there are an infinite number of different-sized infinities.

A neon infinity metaverse symbol. 3D illustration | Infinities Come in Different Sizes — Infinity Asset id: 2118543950 by Sahara Prince

I should say that today Saturday November 8, 2025, is National STEM Day, or STEAM Day. Stem stands for Science, Technology, Engineering, and Mathematics. The extra ‘A’ in STEAM stands for Art. Therefore, I thought that posting something related was appropriate for today, in this case it is Mathematics. I have to admit I am posting it a little bit late in the day though.

To infinity … and beyond!

Madrid, Spain; 05-14-2024: Large figure of the famous character Buzz Lightyear from the movie Toy Story in an exhibition called Pixar World about the studio's films. — Buzz Lightyear “To infinity … and beyond”. Shutterstock Asset id: 2464838811 by MSCT Pics

As mentioned, infinites can have different sizes. How about, for example, the set of all natural numbers and the set of even numbers. After all, it seems like the set of all even numbers should be half as big. As it turns out they are the same size. That’s because for all natural numbers 1, 2, 3, 4, 5 you can always find a buddy, 2, 4, 6, 8, 10 among the even numbers. This is called a bijection. However, you cannot do this with natural numbers versus real numbers. You cannot pair up a natural number with the real numbers because there are infinitely many for each single natural number.

The set of all real numbers is really a larger infinity than natural numbers, which by the way is the smallest infinity. The sets of natural numbers and, for example, even numbers are called countable infinities, and the set of real numbers are called uncountable infinities. In addition, there are infinitely many different sizes of infinities that are larger than both natural numbers and real numbers.

Another interesting, related issue is that Cantor tried to prove that there are no infinities with sizes that lie in between the natural numbers and the real numbers. This was called the continuum hypothesis. As it turned out this hypothesis is not possible to prove (you can prove that it cannot be proved) at the same time as it is not possible to disprove. It is related to Gödels incompleteness theorem but is not the same. However, it is another absolute limit to human knowledge, things we know that we can never know.

If you want to have your mind blown, watch this 8 minute YouTube video about infinities of different sizes and the continuum hypothesis.

Other Mathematics Related Super Facts

To see the other Super Facts click here

Eulers Polyhedra Math Magic

Super fact 64 : V – E + F = 2 is true for all convex polyhedra, where V is the number of vertices (corners), E is the number of edges, and F is the number of faces of a convex polyhedron. This is called Euler’s formula for polyhedra.

Convex polyhedra are polyhedra without holes, or it has no internal angles larger than 180 degrees. To express that exactly; A convex polyhedron is a three-dimensional solid with flat polygonal faces where a line segment connecting any two points on its surface or interior remains entirely within the solid. I can add that convex polyhedra consists of convex polygons as their faces. All its faces are convex polygons.

On the left are three convex polygons and on the left are three concave polygons. — The difference between convex and concave polygons. Notice that the concave polygons on the right have “holes” in them, or inner angles larger than 180 degrees, and that you can draw a line starting and ending inside the polygon that goes outside the polygon.

It is easy to understand that there are an infinite number of convex polyhedra. All pyramids (with convex polygons for bottoms) are convex polyhedra whether the bottom is a square/rectangle, or a convex pentagon, hexagon, heptagon, octagon, or any kind of convex polygon, even with trillions.

A hexagonal pyramid with differently colored faces | Eulers Polyhedra Math Magic | Euler's Polyhedron Formula — A hexagonal pyramid (it is convex). Tomruen at en.wikipedia, Public domain, via Wikimedia Commons.

Examples of convex polyhedra are cubes, boxes, a tetrahedron, pyramids of various sorts, an octahedron, dodecahedron, icosahedron, but there are infinitely many.

As an example, take a cube (like a dice). It has six faces (F = 6), eight vertices (corners V = 8), and 12 edges (V – E + F = 2 or 8 – 12 + 6 = 2). A tetrahedron has four faces (F = 4), four vertices (V =4), and six edges (E = 6) (V – E + F = 2 or 4 – 6 + 4 = 2). A pyramid (with a square bottom) has five faces (F = 5), five vertices (V = 5) and eight edges (E = 8) (V – E + F = 2 or 5 – 8 + 5 = 2). An octahedron has eight faces (F = 8), and six vertices (V = 6), and twelve edges (E = 12) (V – E + F = 2 or 6 – 12 + 8 = 2). A dodecahedron has twelve faces (F = 12), and twenty vertices (V = 20), and thirty edges (E = 30) (V – E + F = 2 or 20 – 30 + 12 = 2). An icosahedron has twenty faces (F = 20), and twelve vertices (V = 20), and thirty edges (E = 30) (V – E + F = 2 or 12 – 30 + 20 = 2). Euler’s Polyhedral Formula works for all of them and for all the infinite number of convex polyhedra that exists.

Line of colorful Platonic solids on a grey surface (polyhedra - tetrahedron, cube, octahedron, dodecahedron and icosahedron, 3d render, banner. — Tetrahedron, cube, octahedron, dodecahedron and icosahedron, Shutterstock Asset id: 2138211027 by Dotted Yeti

I consider this a super fact because it is quite amazing and surprising that the number of faces, vertices, and edges follow the same formula for all convex polyhedra. At least it is surprising if you haven’t seen it before. I should say that Leonhard Euler’s most celebrated discovery is probably his discovery of the Euler Number and the associated Euler’s Formula.

More Polyhedra Examples

The three first examples below are convex polyhedra so Euler’s Polyhedral Formula apply. The last two examples are not so Euler’s Polyhedral Formula does not apply.

Blue truncated icosahedrons. Geometric soccer ball or football shape. Archimedean solid. Regular polygon outline with pentagonal and hexagonal faces. Blue gradient polygonal figure | Eulers Polyhedra Math Magic | Euler's Polyhedron Formula — This is a truncated icosahedron, which is a convex polyhedra, so Euler’s Polyhedral Formula apply. Shutterstock Asset id: 2309812551 by Mima Subota.

A green Rhombicuboctahedron with 8 triangles and 18 squares as faces. — This Rhombicuboctahedron is an example of convex polyhedron, so Euler’s Polyhedral Formula applies. Cyp, CC BY 4.0 <https://creativecommons.org/licenses/by/4.0>, via Wikimedia Commons.

Icosidodecahedron with faces that are triangles and pentagons. — This Icosidodecahedron is another example of a convex polyhedron, so Euler’s Polyhedral Formula applies. Attribution must be given to Robert Webb’s Stella software as the creator of this image along with a link to the website: http://www.software3d.com/Stella.php. A complimentary copy of any book or poster using images from the Software would also be appreciated where feasible., Attribution, via Wikimedia Commons

This polyhedron is donut shaped | Eulers Polyhedra Math Magic | Euler's Polyhedron Formula — This hexagonal torus / toroidal polyhedron is not a convex polyhedra, so Euler’s Polyhedral Formula does not apply in this case. Tom Ruen, SVG version from de:User:Antonsusi, Public domain, via Wikimedia Commons

3d polyhedron Merkaba, esoteric bronze crystal, sacral geometry shape, volume david star, mesh form, abstract vector object — This Merkaba Polyhedron is not a convex polyhedra, so Euler’s Polyhedral Formula does not apply in this case. Shutterstock Asset id: 1296063079 by Panimoni

To see the other Super Facts click here

The Euler Number Math Magic

As I said all this is amazing, mind blowing if you will, if you understand it, which is why I will try to explain it. Why I consider this a super fact is because when you first encounter the Euler number and the Euler formula, and you somewhat understand what it means, it is likely to be a mind-blowing experience. Those among you who have studied higher math, AP math classes in high school, or college level math are probably familiar with what I am about to describe, so your mind may not be blown. By the way you pronounce Euler like “Oiler”.

Euler’s Number and Pi Two Irrational Numbers

Pi is the number you get when you divide the distance around a circle (the circumference) by the distance across the middle (the diameter). The Euler number is a bit more complicated to explain. I will do that next. Both pi and the Euler number are irrational numbers, which means that when written as a decimal, the number neither terminates nor repeats. As I mentioned, both pi and the Euler number are extremely important numbers in math. Perhaps the Euler should have its own day, just like pi has its own day (March 14). Maybe we should start celebrating Euler number day on February 7.

The picture shows a circle and a brief explanation of what pi is. The 20 first decimals of pi as well as the 20 first decimals of the Euler number are shown. — The first 20 decimals of pi and of the Euler number.

Exponents

Before I explain what, the Euler number is, I need to explain what an exponent is. If you multiply a number by itself x number of times, then x is the exponent. If you multiply two by itself four times 2*2*2*2, called 2 raised to 4, then 4 is the exponent. By the way the answer is 2^4 = 16 (called 2 raised to 4 is 16). I hope the illustration below will explain it.

This picture explains what an exponent is. — Overview of exponents.

And finally, before explaining what the Euler number is I should also mention what a factorial is. The factorial of a number is the product of all positive integers less than or equal to that number. The factorial of 5 is denoted 5! and is 1*2*3*4*5 = 120. Also, the factorial of 0 or 0! = 1 (per definition).

Definition of the Euler Number

One more thing I need to explain before I go ahead with the definition for the Euler number is what is meant by allowing a number n in a formula to go towards infinity (limit –> infinity). Let’s say you have a formula that contains the number n. If the value of the formula does not change much as n becomes very large than it might be approaching a specific number as n approaches infinity. You say that it approaches a limit. I am trying to illustrate this in the picture below.

The formula (1 + 1/n)^n is given for a lot of different numbers n. You can see that a number, a limit, is reached as n approaches infinity | The Euler Number Math Magic — As the number n gets bigger the formula stops getting bigger and instead approaches a limit. When n approaches infinity that will be a very specific number. Which number do you think it is?

The picture features the definition of Euler’s Number as well as another formula consisting of an infinite sum that is also Euler’s number. — The definition of Euler’s number plus an infinite series sum that is also the same as Euler’s number.

Two formulas equal to Euler’s Number. One is an exponent approaching infinity and the other is a sum from 0 to infinity | The Euler Number Math Magic — Definition of the Euler’s constant in two different ways, Asset id: 1227561829, by benjaminec.

Euler’s Number in Calculus

As I mentioned, Euler’s number shows up in mathematics in a lot of places. It is an extremely useful number with some amazing properties and that includes calculus. However, explaining functions and calculus may be going a bit too far, so I am just going to simply state that the derivate of e^x is just e^x and the indefinite integral, or the anti-derivative of e^x is e^x. In other words, differentiation / integration does not change this function. It also means that the slope of the curve is the same as the curve itself. Among all the infinite number of functions this is only true for e^x.

Differentiation and integration formulas for the exponential function. — Differentiation and integration does not change the function e^x.

Trigonometric Functions

Next, I would like to launch into Euler’s formula. However, before I do that, I need to explain what trigonometric functions and imaginary numbers are. The trigonometric function sin(x) is the ratio of the length of the side opposite to a given angle to the length of the hypotenuse. In other words, if the hypotenuse is equal to 1, then sin(x) is the length of the opposite side to the given angle. The trigonometric function cos(x) is the ratio of the side of the triangle adjacent to the angle divided by the hypotenuse. In other words, if the hypotenuse is equal to 1, then cos(x) is the length of the adjacent side to the given angle.

Sin and cos are always between 1 and -1. ‘x’ is often expressed in degrees going from 0 to 360 (or 0 to 90 in a right-angled triangle). However, there is another way to express angles in triangles and that is radians. In this case the number pi corresponds to 180 degrees, pi/2 corresponds to 90 degrees, pi/4 corresponds to 45 degrees, etc. Euler’s formula uses trigonometric functions, but it only works if you use pi instead of degrees. Pi and Euler’s number have a special relationship. Sin and cos are illustrated in the picture below.

The picture shows a right-angled triangle with the sides being the hypotenuse set to 1 and the two other sides sin(x) and cos(x) respectively | The Euler Number Math Magic — Illustration of the trigonometric functions sin(x) and cos(x).

Imaginary Numbers

The last thing I need to explain before demonstrating Euler’s formula is imaginary numbers. The square root of a number is another number that, when multiplied by itself, equals the original number. For example, the square root of 4 is 2, because 2 * 2 = 4. The square root of 9 is 3, because 3 * 3 = 9. As long as you deal with real numbers, square roots must be positive numbers because you cannot multiply two numbers and get a negative number. -2 * -2 is 4, not -4.

However, that did not stop some mathematicians from making up a square root that was negative. This imaginary number is the square root of -1 and is referred to as i, yes just i, for imaginary. So, what’s the point of making up numbers that can’t exist? Well, it turned out to be quite useful and you can manipulate imaginary numbers to result in real numbers. For example, if you multiply the imaginary number i by itself i*i you get -1. If you multiply i by itself four times, in other words i^4, or i raised to 4, you get 1. Even more impressively, i raised to i, or i^i, is a real number. i^i = 0.207879… This is illustrated in the picture below.

The picture features the definition of the imaginary number and an explanation for what imaginary numbers are, as well as examples. — Imaginary numbers illustrated

Eulers Formula

Without giving the proof, or any detailed explanations, below is Euler’s identity and Euler’s Formula (e^ix = cos(x) + isin(x)). Notice the mix of Euler’s number, pi, the trigonometric functions using radians (based on pi), and the imaginary number. Well, likely mind-blown, if you have not seen it already and you understood this post up to here.